
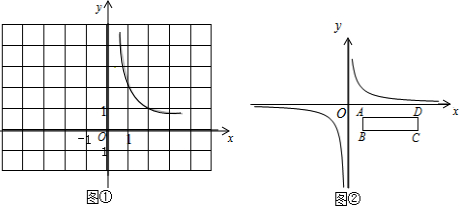
分析 (1)根据图象向右平移减,可得答案;
(2)根据图象向左平移加,可得答案;
(3)①根据图象向右平移减,最先经过B点,最后经过D点,可得答案;
②根据图形的割补法,可得规则的图形,根据面积的和差,可得答案.
解答 解:(1)一次函数y=x-1的图象是由正比例函数y=x图象向 右平移1个单位长度得到,
故答案为:右,1;
(2)如图1: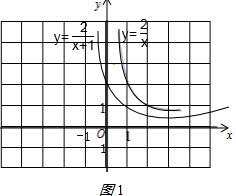 ,
,
函数y=$\frac{2}{x+1}$的图象是由函数y=$\frac{2}{x}$图象经向左平移一个单位得到的.
(3)①当函数y=$\frac{2}{x}$的图象经过点B时,函数解析式为y=$\frac{2}{x-2}$,
当函数y=$\frac{2}{x}$的图象经过点D时,函数解析式为y=$\frac{2}{x-6}$,
由函数图象平移规律得2≤t≤6;
②如图2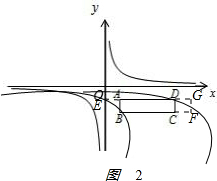 图形是AEBFD,
图形是AEBFD,
图形ABE向右平移3个单位,得图形DGF,
图形DGF与图形CDF组合成边长为1的正方形CFGD,
S=3×1+1×1=4.
点评 本题考查了反比例函数综合题,利用了图象平移的方法:图象向右平移减,向左平移加是解题关键,又利用了图形的割补法得出规则的图形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
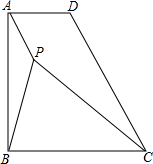 已知在直角梯形ABCD中,∠ABC=90°,AB=BC,点P是梯形内一点,且PA=1,PB=2,PC=3
已知在直角梯形ABCD中,∠ABC=90°,AB=BC,点P是梯形内一点,且PA=1,PB=2,PC=3查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com