
分析 (1)以AD为直径画圆与BC交于点P1、P2,则点P1、P2为所求点;
(2)由矩形的性质得到AD=BC=10,AB=CD=4根据三角形相似即可解出;
(3)由三角形的中位线得到EF∥BC,$EF=\frac{1}{2}BC=6$,根据EF与BC间距离为3,推出以EF为直径的⊙O与BC相切,得出BC上符合条件的点Q只有一个,记⊙O与BC相切于点Q,连接OQ,过点E作EG⊥BC,垂足为G,证出四边形EOQG为正方形,由勾股定理即可求出.
解答 解: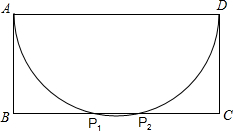 (1)如图所示,则点P1、P2为所求点;
(1)如图所示,则点P1、P2为所求点;
(2)在矩形ABCD中,AD=BC=10,AB=CD=4,
设BP=x,则PC=10-x,
∵∠APD=90°,
∴∠APB+∠CPD=90°,
∵∠BAP+∠APB=90°,
∴∠BAP=∠CPD,
又∵∠B=∠C=90°,
∴△ABP∽△PCD,
∴$\frac{AB}{PC}=\frac{BP}{CD}$,
∴$\frac{4}{10-x}=\frac{x}{4}$,
解得:x1=2,x2=8,
∴BP的长是2或8;
(3)如图:
∵EF分别为AB、AC的中点,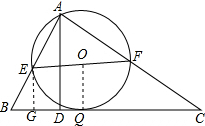
∴EF∥BC,$EF=\frac{1}{2}BC=6$,
∵AD=6,AD⊥BC,
∴EF与BC间距离为3,
∴以EF为直径的⊙O与BC相切,
∴BC上符合条件的点Q只有一个,记⊙O与BC相切于点Q,
连接OQ,过点E作EG⊥BC,垂足为G,
∴EG=OE=3,
∴四边形EOQG为正方形,
在Rt△EBG中,∠B=60°,EG=3,∴$BG=\sqrt{3}$,∴$BQ=3+\sqrt{3}$.
点评 本题考查了基本作图,矩形的性质,相似三角形的判定和性质,三角形的中位线定理,找准BC上符合条件的点Q只有一个是解题的关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
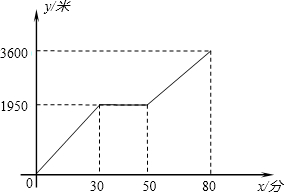 小华和小晶上山游玩,小华步行,小晶乘坐缆车,相约在山顶缆车的终点会合.已知小华步行的路程是缆车所经线路长的2倍,小晶在小华出发后50分钟才坐上缆车,缆车的平均速度为每分钟180米.图中的折线反映了小华行走的路程y(米)与时间x(分钟)之间的函数关系.
小华和小晶上山游玩,小华步行,小晶乘坐缆车,相约在山顶缆车的终点会合.已知小华步行的路程是缆车所经线路长的2倍,小晶在小华出发后50分钟才坐上缆车,缆车的平均速度为每分钟180米.图中的折线反映了小华行走的路程y(米)与时间x(分钟)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | 甲种客车 | 乙种客车 |
| 载客量(人/辆) | 45 | 30 |
| 租金(元/辆) | 1000 | 800 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
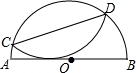 半圆⊙O中,AB为直径,C、D为半圆上任意两点,将$\widehat{CD}$沿直线CD翻折使AB与$\widehat{CD}$相切,已知AB=8,求CD的最大值4$\sqrt{3}$.
半圆⊙O中,AB为直径,C、D为半圆上任意两点,将$\widehat{CD}$沿直线CD翻折使AB与$\widehat{CD}$相切,已知AB=8,求CD的最大值4$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com