
【题目】已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.
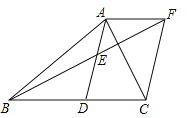
(1)求证:四边形ADCF是平行四边形;
(2)当AB与AC有何数量关系时,四边形ADCF为矩形,请说明理由.
【答案】(1)证明见解析,(2)当AB=AC时,四边形ADCF为矩形,理由见解析.
【解析】试题(1)可证△AFE≌△DBE,得出AF=BD,进而根据AF=DC,得出D是BC中点的结论;
(2)若AB=AC,则△ABC是等腰三角形,根据等腰三角形三线合一的性质知AD⊥BC;而AF与DC平行且相等,故四边形ADCF是平行四边形,又AD⊥BC,则四边形ADCF是矩形.
试题解析:(1)证明:∵E是AD的中点,
∴AE=DE.
∵AF∥BC,
∴∠FAE=∠BDE,∠AFE=∠DBE.
在△AFE和△DBE中, 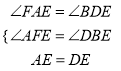 ,
,
∴△AFE≌△DBE(AAS).
∴AF=BD.
∵AF=DC,
∴BD=DC.
即:D是BC的中点.
(2)AB=AC,理由如下:
∵AF=DC,AF∥DC,
∴四边形ADCF是平行四边形.
∵AB=AC,BD=DC,
∴AD⊥BC即∠ADC=90°.
∴平行四边形ADCF是矩形.


科目:初中数学 来源: 题型:
【题目】某公园准备修建一块长方形草坪,长为30米,宽为20米.并在草坪上修建如图所示的十字路,已知十字路宽![]() 米,回答下列问题:
米,回答下列问题:
(1)修建十字路的面积是多少平方米?
(2)草坪(阴影部分)的面积是多少?
(3)如果十字路宽2米,那么草坪(阴影部分)的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C. 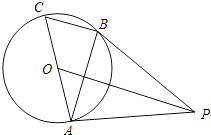
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字. 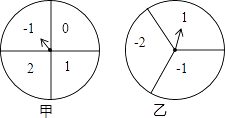
(1)直接写出转动甲盘停止后指针指向数字“1”的概率;
(2)小华和小明利用这两个转盘做游戏,两人分别同时转动甲、乙两个转盘,停止后,指针各指向一个数字,若两数字之积为非负数则小华胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
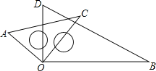
【题目】如图,将两块三角板的顶点重合.
(1)请写出图中所有以![]() 点为顶点且小于平角的角;
点为顶点且小于平角的角;
(2)你写出的角中相等的角有________;
(3)若![]() ,试求
,试求![]() 的度数;
的度数;
(4)当三角板![]() 绕点
绕点![]() 适当旋转(保持两三角板有重合部分)时,
适当旋转(保持两三角板有重合部分)时,![]() 与
与![]() 之间具有怎样的数量关系?
之间具有怎样的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
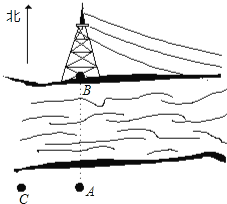
【题目】如图所示,小刚站在河边的A点处,在河对面(小刚的正北方向)的B处有一电视塔,小刚想知道电线塔离他有多远,于是他向正西走了20步到达一棵树C处,接着继续向前走了20步到达D处,然后他左转90°直行,当他看到的电线塔B,树C和自己所处的位置E在一条直线上时,他在整个步测过程中共走了100步.
(1)根据题意,画出示意图;
(2)如果小刚的一步大约有50cm长,请你估计小刚的初始位置A与电线塔B之间的距离,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
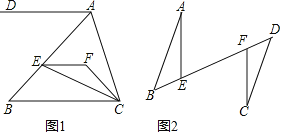
【题目】(1)如图1,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数;
(2)如图2,AB∥CD,AB=CD,BF=DE,求证:∠AEF=∠CFB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q. 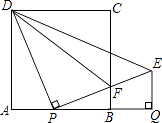
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,数学家高斯在上学时曾经研究过这样一个问题,1+2+3+…+10=?经过研究,这个问题的一般性结论是1+2+3+…+n=![]() n(n+1),其中n为正整数,现在我们来研究一个类似的问题:1×2+2×3+…+ n(n+1)=?
n(n+1),其中n为正整数,现在我们来研究一个类似的问题:1×2+2×3+…+ n(n+1)=?
观察下面三个特殊的等式:
1×2=![]() (1×2×3-0×1×2)
(1×2×3-0×1×2)
2×3=![]() (2×3×4-1×2×3)
(2×3×4-1×2×3)
3×4=![]() (3×4×5-2×3×4)
(3×4×5-2×3×4)
将这三个等式的两边相加,可以得到1×2+2×3+3×4=![]() ×3×4×5=20.
×3×4×5=20.
读完这段材料,请你计算:
(1)1×2+2×3+…+100×101;
(2)1×2+2×3+…+ n(n+1);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com