
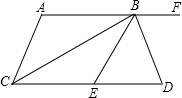
 如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由BC⊥BD得到∠CBE+∠DBE=90°,∠BCD+∠D=90°,则可对②选项进行判断;再由平行线的性质得∠D=∠DBF,由角平分线定义得∠DBF=∠DBE,则∠CBE=∠BCE,而∠ABC=∠BCE,所以∠ABC=∠CBE,则可对①选项进行判断;接着由BC平分∠ACD得到∠ACB=∠BCE,所以∠ACB=∠CBE,根据平行线的判定即可得到AC∥BE,于是可对③选项进行判断;利用平行线的性质得到∠DEB=∠ABE=2∠ABC,加上∠D=∠DBE=∠DBF,∠D≠∠BED,于是可得∠DBF≠2∠ABC,则可对④选项进行判断.
解答 解:①∵BC⊥BD,
∴∠DBE+∠CBE=90°,∠ABC+∠DBF=90°,
又∵BD平分∠EBF,
∴∠DBE=∠DBF,
∴∠ABC=∠CBE,
即BC平分∠ABE,
故①正确;
②∵BC⊥BD,
∴∠CBD=90°,
∴∠BCD+∠D=90°,
故②正确;
③由AB∥CE,
∴∠ABC=∠BCE,
BC平分∠ABE、∠ACE,
∴∠ABC=∠CBE,∠ACB=∠BCE,
∴∠ACB=∠CBE,
∴AC∥BE,
故③正确;
④∵∠DEB=∠ABE=2∠ABC,
而∠D=∠DBE=∠DBF,
∠D≠∠BED,
∴∠DBF≠2∠ABC,故④错误.
故选C.
点评 本题考查了平行线的性质和判定,垂直定义,角平分线定义,三角形的内角和定理的应用,能综合运用性质进行推理是解此题的关键,


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:填空题
 如图,已知:在?ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.
如图,已知:在?ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点O、A在数轴上表示的数分别是0,0.1,将线段OA分成100等份,其分点由左向右依次为M1,M2…M99,再将线段OM1分成100等份,其分点由左向右依次为N1,N2,…N99,则点N15所表示的数用科学记数法表示为1.5×10-4.
如图,点O、A在数轴上表示的数分别是0,0.1,将线段OA分成100等份,其分点由左向右依次为M1,M2…M99,再将线段OM1分成100等份,其分点由左向右依次为N1,N2,…N99,则点N15所表示的数用科学记数法表示为1.5×10-4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 有三个角是直角的四边形是矩形 | |
| C. | 有两条边相等的四边形是平行四边形 | |
| D. | 四条边都相等的平行四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
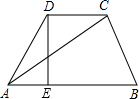 如图,在梯形ABCD中,DC∥AB,DE⊥AB,DC=2,AC=$\sqrt{19}$,∠DAE=60°,则DE=$\frac{3\sqrt{3}}{2}$.
如图,在梯形ABCD中,DC∥AB,DE⊥AB,DC=2,AC=$\sqrt{19}$,∠DAE=60°,则DE=$\frac{3\sqrt{3}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com