
【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;
(4)你能用一句简洁的话,描述你发现的结论吗?
![]()
【答案】(1)7;(2)![]() a;(3)
a;(3)![]() b;(4)答案见解析
b;(4)答案见解析
【解析】试题分析:(1)根据M、N分别是AC、BC的中点,我们可得出MC、NC分别是AC、BC的一半,那么MC、CN的和就应该是AC、BC和的一半,也就是说MN是AB的一半,有了AC、CB的值,那么就有了AB的值,也就能求出MN的值了;
(2)方法同(1)只不过AC、BC的值换成了AC+CB=acm,其他步骤是一样的;
(3)当C在线段AB的延长线上时,根据M、N分别是AC、BC的中点,我们可得出MC、NC分别是AC、BC的一半.于是,MC、NC的差就应该是AC、BC的差的一半,也就是说MN是AC-BC即AB的一半.有AC-BC的值,MN也就能求出来了;
(4)综合上面我们可发现,无论C在线段AB的什么位置(包括延长线),无论AC、BC的值是多少,MN都恒等于AB的一半.
解:(1)MN=MC+NC=![]() AC+
AC+![]() BC=
BC=![]() (AC+BC)=
(AC+BC)=![]() ×(8+6)=
×(8+6)=![]() ×14=7;
×14=7;
(2)MN=MC+NC=![]() AC+
AC+![]() BC=
BC=![]() (AC+BC)=
(AC+BC)=![]() a;
a;
(3)MN=MC-NC=![]() AC-
AC-![]() BC=
BC=![]() (AC-BC)=
(AC-BC)= ![]() b;
b;
(4)如图,只要满足点C在线段AB所在直线上,点M、N分别是AC、BC的中点.那么MN就等于AB的一半.
![]()


科目:初中数学 来源: 题型:
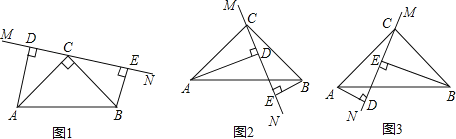
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,
BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,请写出DE、AD、BE之间的等量关系并加以证明.
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE之间又有怎样的等量关系?请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
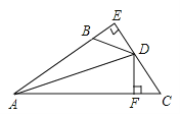
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,∠ABD与∠C互补.
(1)求证:AD平分∠BAC;(2)若AB=5,AC=9,则AE=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
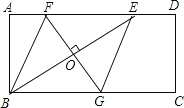
【题目】如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=![]() AD (n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
AD (n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=a(a为常数),n=3时,求FG的长;
(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当![]() 时,求n的值.(直接写出结果,不必写出解答过程)
时,求n的值.(直接写出结果,不必写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调、冰箱、彩电共360台,且彩电至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表:
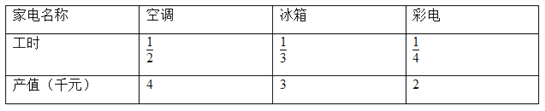
问每周应生产空调、冰箱、彩电各多少台,才能使产值最高?最高产值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com