练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：如图在中，过对角线的中点作直线分别交的延长线、的延长线于点

    （1）观察图形并找出一对全等三角形：____________________，请加以证明；

    （2）在（1）中你所找出的一对全等三角形，其中一个三角形可由另一个三角形经过怎样的变换得到？

     


    （1）；

    证明：∵四边形是平行四边形
    　　　　 ∴

    ∴

    又∵

    ∴

    证明：∵四边形是平行四边形
    　　　　 ∴

    ∴

    又∵

    ∴

    ；2分

    证明：∵四边形是平行四边形
    　　　　 ∴

    又∵

    ∴

    （2）绕点旋转后得到或以点为中心作对称变换得到．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知：如图，在直角坐标系中，以点M（1，0）为圆心、直径AC为2
    		2
    的圆与y轴交于A、D两点．
    （1）求点A的坐标；
    （2）设过点A的直线y=x+b与x轴交于点B．探究：直线AB是否⊙M的切线并对你的结论加以证明；
    （3）在（2）的前提下，连接BC，记△ABC的外接圆面积为S1、⊙M面积为S2，若
    S1
    S2
    =
    h
    4
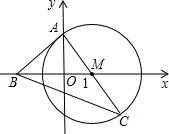    ，抛物线y=ax2+bx+c精英家教网经过B、M两点，且它的顶点到x轴的距离为h．求这条抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图，在平面直角坐标系xOy中，直线y=-
    34
    x+6    与x轴、y轴的交点分别为A、B两点，将∠OBA对折，使点O的对应点H落在直线AB上，折痕交x轴于点C．
    （1）直接写出点C的坐标，并求过A、B、C三点的抛物线的解析式；
    （2）若（1）中抛物线的顶点为D，在直线BC上是否存在点P，使得四边形ODAP为平行四边形？若存在，求出点P的坐标；若不存在，说明理由；
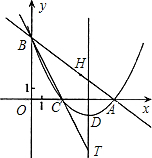    （3）若把（1）中的抛物线向左平移3.5个单位，则图象与x轴交于F、N（点F在点N的左侧）两点，交y轴于E点，则在此抛物线的对称轴上是否存在一点Q，使点Q到E、N两点的距离之差最大？若存在，请求出点Q的坐标；精英家教网若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：鼎尖助学系列—同步练习(数学 九年级下册)、逆命题、逆定理(2) 题型：047

    已知：如图甲中，BD、CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F、G，连结FG，延长AF、AG，与直线BC相交，易证．若 甲BD、CE分别△ABC的内角平分线(如图丁)；(丁)BD为△ABC的内角平分线，CE为△ABC的外角平分线(如图(乙))，则在图(丁)、图(乙)两种情况下，线段FG与△ABC的三边又有怎样的数量关系？请写出猜想，并对其中的一种情况给予证明．

    s

    查看答案和解析>>

    科目：初中数学 来源：同步练习　　数学九年级下册 题型：044

    已知：如图(1)中，BD、CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F、G，连结FG，延长AF、AG，与直线BC相交，易证FG＝(AB＋BC＋AC)．若(1)BD、CE分别△ABC的内角平分线(如图(2))；(2)BD为△ABC的内角平分线，CE为△ABC的外角平分线(如图(3))，则在图(2)、图(3)两种情况下，线段FG与△ABC的三边又有怎样的数量关系？请写出猜想，并对其中的一种情况给予证明．

    查看答案和解析>>

    科目：初中数学 来源：2013-2014学年山东青岛市崂山区九年级第一学期期末考试数学试卷（解析版） 题型：解答题

    已知：如图,△ABC中,点D、E分别为BC、AC边中点,连接AD,连接DE,过A点作AF∥BC,交DE的延长线于F.连接CF,

    （1）求证：四边形ADCF是平行四边形；

    （2）对添加一个条件               ,使得四边形ADCF是矩形,并进行证明；

    （3）在（2）的基础上对再添加一个条件              ,使得四边形ADCF是正方形,不必证明.

     

    查看答案和解析>>

    同步练习册答案