练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．若a-b=2，a-c=1，则（2a-b-c）2+（c-a）2-（b-c）2=11．．

    分析 先将2a-b-c，c-a，b-c的值分别求出，然后代入原式即可求出答案．

    解答 解：∵a-b=2，a-c=1，
    ∴c-a=-1
    a-b+a-c=3，即2a-b-c=3，
    （a-c）-（a-b）=-1，即c-b=-1，
    ∴原式=32+（-1）2+（-1）2=11
    故答案为：11

    点评 本题考查整式的运算，解题的关键是先将2a-b-c，c-a，b-c的值分别求出，本题属于中等题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    2．下列运算正确的是（　　）
    A．（a2）3=a5B．a2•a3=a5C．a-1=-aD．（a+b）（a-b）=a2+b2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．小明的爸爸是个“健步走”运动爱好者，他用手机软件记录了某个月（30天）每天健步走的步数，并将记录结果绘制成了如下统计表：
    步数（万步）1.11.21.31.41.5
    天数375123
    在每天所走的步数这组数据中，众数和中位数分别是1.4，1.35．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算：$\sqrt{24}$×$\sqrt{\frac{1}{3}}$+|-2|-4sin45°-${（\frac{1}{3}）}^{-1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

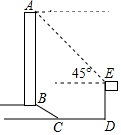    20．如图所示，广场有一纪念碑，其正前方恰有一个高度为15米的临时观侧台ED，从观测台顶端E处侧得纪念碑顶端A的仰角a是45°，观测台底端D到纪念碑底座边沿C的距离DC是20米，底座BC部分的坡长是12米，其坡度i=1：$\sqrt{3}$，求该纪念碑的高度．（结果精确到0.1米，参考数据：$\sqrt{2}≈1.41$，$\sqrt{3}≈1.73$，$\sqrt{6}≈2.45$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

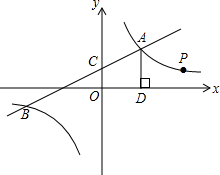    10．如图，一次函数y1=k1x+b与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A（4，m）和B（-8，-2），与y轴交于点C．
    （1）m=4，k1=$\frac{1}{2}$；
    （2）当x的取值是-8＜x＜0或x＞4时，k1x+b＞$\frac{{k}_{2}}{x}$；
    （3）过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点．设直线OP与线段AD交于点E，当S四边形ODAC：S△ODE=3：1时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．在平面直角坐标系中，反比例函数y=$\frac{m}{x}$（x＞0）的图象上有一点A（a，3），过点A作AB⊥x轴于点B，将点B沿x轴正方向平移2个单位长度得到点C，过点C作y轴的平行线交反比例函数于点D，CD=$\frac{3}{2}$，直线AD与x轴交于点M，与y轴交于点N．
    （1）用含a的式子表示点D的横坐标为：a+2；
    （2）求a的值和直线AD的函数表达式；
    （3）请判断线段AN与MD的数量关系，并说明理由；
    （4）若一次函数y1=k1x+b1经过点（10，9），与双曲线y=$\frac{m}{x}$（x＞0）交于点P，且该一次函数y1的值随x的增大而增大，请确定P点横坐标n的取值范围（不必写出过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．函数y=$\frac{\sqrt{2x-4}}{x-3}$中自变量x的取值范围是x≥2且x≠3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

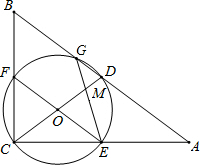    15．如图，在△ABC中，∠ACB=90°，D是AB的中点，以DC为直径的⊙O交△ABC的三边，交点分别是G、F、E点，GE，CD的交点为M，且ME=4$\sqrt{6}$，MD：CO=2：5．
    （1）求证：∠GEF=∠A；
    （2）求⊙O的直径CD的长．

    查看答案和解析>>

    同步练习册答案