
【题目】在二次函数y=-x2+bx+c中,函数y与自变量x的部分对应值如下表:
x | …… | -2 | 0 | 3 | 4 | …… |
y | …… | -7 | m | n | -7 | …… |
则m、n的大小关系为( )
A. m>n B. m<n C. m=n D. 无法确定
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
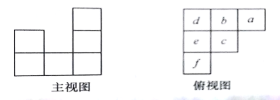
【题目】用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:
(1)求![]() 的值;
的值;
(2)这个几何体最少有几个小立方体搭成,最多有几个小立方体搭成;
(3)当![]() 时画出这个几何体的左视图.
时画出这个几何体的左视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
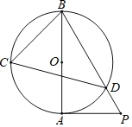
【题目】如图AB是⊙O的直径,PA与⊙O相切于点A,BP与⊙O相交于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60°.
(1)求∠ABD的度数;
(2)若AB=6,求PD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
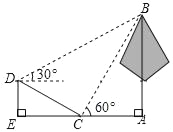
【题目】如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知DE⊥EA,斜坡CD的长度为30m,DE的长为15m,则树AB的高度是_____m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
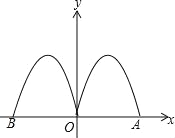
A. 0<m<![]() B.
B. ![]() <m<
<m<![]()
C. 0<m<![]() D. m<
D. m<![]() 或m<
或m<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
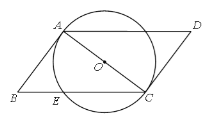
【题目】如图,AC是⊙O的直径,AB与⊙O相切于点A.四边形ABCD是平行四边形,BC交⊙O于点E.
(1)证明直线CD与⊙O相切;
(2)若⊙O的半径为5 cm,弦CE的长为8 cm,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2=![]() 的图象交于点A(﹣1,3)、B(n,﹣1).
的图象交于点A(﹣1,3)、B(n,﹣1).
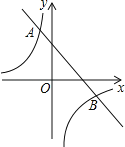
(1)求反比例函数的解析式;
(2)当y1>y2时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
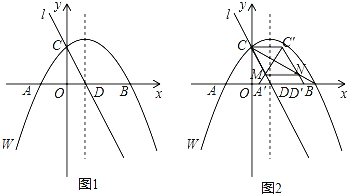
【题目】综合与探究
如图1,在平面直角坐标系xOy中,抛物线W的函数表达式为y=﹣![]() x2+
x2+![]() x+4.抛物线W与x轴交于A,B两点(点B在点A的右侧,与y轴交于点C,它的对称轴与x轴交于点D,直线l经过C、D两点.
x+4.抛物线W与x轴交于A,B两点(点B在点A的右侧,与y轴交于点C,它的对称轴与x轴交于点D,直线l经过C、D两点.
(1)求A、B两点的坐标及直线l的函数表达式.
(2)将抛物线W沿x轴向右平移得到抛物线W′,设抛物线W′的对称轴与直线l交于点F,当△ACF为直角三角形时,求点F的坐标,并直接写出此时抛物线W′的函数表达式.
(3)如图2,连接AC,CB,将△ACD沿x轴向右平移m个单位(0<m≤5),得到△A′C′D′.设A′C交直线l于点M,C′D′交CB于点N,连接CC′,MN.求四边形CMNC′的面积(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
用户月用水量频数分布表 | ||
平均用水量(吨) | 频数 | 频率 |
3~6吨 | 10 | 0.1 |
6~9吨 | m | 0.2 |
9~12吨 | 36 | 0.36 |
12~15吨 | 25 | n |
15~18吨 | 9 | 0.09 |

请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=__ __,n=__ __;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com