
分析 (1)根据有理数的加法和减法可以解答本题;
(2)根据有理数的乘除法和减法可以解答本题;
(3)根据乘法分配律和有理数的加减法可以解答本题;
(4)根据幂的乘方、有理数的加减法可以解答本题.
解答 解:(1)(-0.9)+(+4.4)+(-8.1)+(+5.6)
=(-0.9)+4.4+(-8.1)+5.6
=1;
(2)-3$\frac{1}{2}$×(-$\frac{6}{7}$)-(-10)÷(-$\frac{2}{3}$)
=$-\frac{7}{2}×(-\frac{6}{7})-10×\frac{3}{2}$
=3-15
=-12;
(3)-1-48×($\frac{5}{24}$-$\frac{3}{16}$+$\frac{1}{6}$)
=-1-$48×\frac{5}{24}+48×\frac{3}{16}-48×\frac{1}{6}$
=-1-10+15-8
=-4;
(4)-32-[(-3)2×(-$\frac{4}{3}$)-(-2)3]
=-9-[9×($-\frac{4}{3}$)-(-8)]
=-9-[-12+8]
=-9-(-4)
=-9+4
=-5.
点评 本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
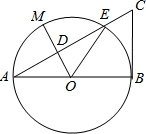 如图,以线段AB为直径的⊙O交线段AC于点E,点M是$\widehat{AE}$ 的中点,OM交AC于点D,BC=2$\sqrt{3}$,∠BOE=60°,∠C=60°.
如图,以线段AB为直径的⊙O交线段AC于点E,点M是$\widehat{AE}$ 的中点,OM交AC于点D,BC=2$\sqrt{3}$,∠BOE=60°,∠C=60°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口向下 | B. | 对称轴是y轴 | ||
| C. | 当x>0时,y随x的增大而减小 | D. | 函数有最小值 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM=8cm,ON=6cm.则该圆玻璃镜的直径是10cm.
如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM=8cm,ON=6cm.则该圆玻璃镜的直径是10cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com