
(1)已知(x+1)( +ax+5)=
+ax+5)= +b
+b +3x+5,求a与b的值;
+3x+5,求a与b的值;
(2)已知(x+ay)(x+by)= -4xy+6
-4xy+6 ,求3(a+b)-2ab的值.
,求3(a+b)-2ab的值.
|
(1)解法一: 原等式可化为  +a +a  +5x+ +5x+ +ax+5= +ax+5= +b +b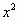 +3x+5, +3x+5,
即  +(a+1) +(a+1) +(a+5)x+5= +(a+5)x+5= +b +b +3x+5. +3x+5.
比较系数得  解得 解得
解法二:原等式是关于x的恒等式,即无论x取何值都能确定a、b的值.因此,可令x取较小的方便计算的值代入.求a、b两个字母的取值,需两个关于a、b的方程组成方程组. 令x=1,得2a-b=-3. 令x=-1,得0=b+1. ∴  解得 解得
(2)由已知,得  +(a+b)xy+ab +(a+b)xy+ab = = -4xy+6 -4xy+6 . .
由多项式相等,则对应项系数相等,得 a+b=-4,ab=6. ∴3(a+b)-2ab=3×(-4)-2×6=-24. |
|
(1)根据两个多项式相等,则两个多项式的对应项相等,两个对应项相等,则对应项的系数相等,由此得到关于a、b的方程(组).(2)可以通过已知条件直接求出(a+b)与ab的值,然后代入要求的结果,所以不要把所求代数式变形. |


科目:初中数学 来源: 题型:
 4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.
4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com