
 荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:
荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:分析 (1)根据函数图象,利用待定系数法求解可得;
(2)设日销售利润为w,分1≤t≤40和41≤t≤80两种情况,根据“总利润=每千克利润×销售量”列出函数解析式,由二次函数的性质分别求得最值即可判断;
(3)求出w=2400时x的值,结合函数图象即可得出答案;
(4)依据(2)中相等关系列出函数解析式,确定其对称轴,由1≤t≤40且销售利润随时间t的增大而增大,结合二次函数的性质可得答案.
解答 解:(1)设解析式为y=kt+b,
将(1,198)、(80,40)代入,得:
$\left\{\begin{array}{l}{k+b=198}\\{80k+b=40}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=200}\end{array}\right.$,
∴y=-2t+200(1≤x≤80,t为整数);
(2)设日销售利润为w,则w=(p-6)y,
①当1≤t≤40时,w=($\frac{1}{4}$t+16-6)(-2t+200)=-$\frac{1}{2}$(t-30)2+2450,
∴当t=30时,w最大=2450;
②当41≤t≤80时,w=(-$\frac{1}{2}$t+46-6)(-2t+200)=(t-90)2-100,
∴当t=41时,w最大=2301,
∵2450>2301,
∴第30天的日销售利润最大,最大利润为2450元.
(3)由(2)得:当1≤t≤40时,
w=-$\frac{1}{2}$(t-30)2+2450,
令w=2400,即-$\frac{1}{2}$(t-30)2+2450=2400,
解得:t1=20、t2=40,
由函数w=-$\frac{1}{2}$(t-30)2+2450图象可知,当20≤t≤40时,日销售利润不低于2400元,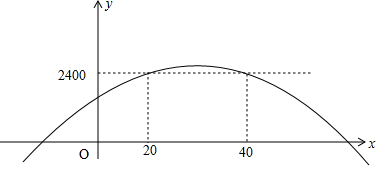
而当41≤t≤80时,w最大=2301<2400,
∴t的取值范围是20≤t≤40,
∴共有21天符合条件.
(4)设日销售利润为w,根据题意,得:
w=($\frac{1}{4}$t+16-6-m)(-2t+200)=-$\frac{1}{2}$t2+(30+2m)t+2000-200m,
其函数图象的对称轴为t=2m+30,
∵w随t的增大而增大,且1≤t≤40,
∴由二次函数的图象及其性质可知2m+30≥40,
解得:m≥5,
又m<7,
∴5≤m<7.
点评 本题主要考查二次函数的应用,熟练掌握待定系数求函数解析式、由相等关系得出利润的函数解析式、利用二次函数的图象解不等式及二次函数的图象与性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一.2016年全国谷子种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg,请解答下列问题:
“春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一.2016年全国谷子种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为$\frac{\sqrt{5}-1}{2}$.
如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为$\frac{\sqrt{5}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
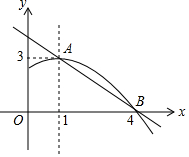 如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5000.3 | B. | 4999.7 | C. | 4997 | D. | 5003 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com