
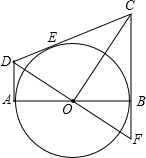
 如图,从圆O外的两点C和D分别引圆的两条切线DA,DC,CB,切点分别是A、E和B,AB是圆O的直径,连接OC、OD,延长DO交CB的延长线于点F,给出如下结论:①AD+BC=CD;②OD2=DE•CD;③CO=DF;④△AOD∽△BCO,其中正确的是①②④.(把所有正确的序号都填在横线上).
如图,从圆O外的两点C和D分别引圆的两条切线DA,DC,CB,切点分别是A、E和B,AB是圆O的直径,连接OC、OD,延长DO交CB的延长线于点F,给出如下结论:①AD+BC=CD;②OD2=DE•CD;③CO=DF;④△AOD∽△BCO,其中正确的是①②④.(把所有正确的序号都填在横线上). 分析 ①根据切线长定理得出;
②连接OE,证明△DOE∽△DCO,列比列式;
③画图说明;
④利用两角相等证明两三角形相似.
解答 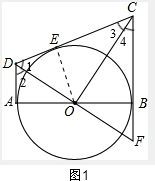 解:①∵DA,DC,CB为⊙O的切线,切点分别是A、E和B,
解:①∵DA,DC,CB为⊙O的切线,切点分别是A、E和B,
∴AD=DE,EC=BC
∴AD+BC=DE+EC=CD,
故选项①正确;
②如图1,连接OE,则OE⊥DC,
由切线可知:∠DAB=∠CBA=90°,∠1=∠2,∠3=∠4,
∴∠ADC+∠BCD=90°,∠1+∠3=90°,
∴∠DOC=90°,
∵∠1=∠1,∠DOC=∠DEO=90°,
∴△DOE∽△DCO,
∴$\frac{OD}{CD}=\frac{DE}{OD}$,
∴OD2=DE•CD,
故选项②正确;
③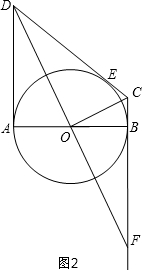 如图1和图2,因为C和D为两个动点,发现随着C的改变,CO的长也随之改变,点C离点B的距离越近,CO越短,但DF越长,所以CO≠DF;
如图1和图2,因为C和D为两个动点,发现随着C的改变,CO的长也随之改变,点C离点B的距离越近,CO越短,但DF越长,所以CO≠DF;
故选项③不正确;
④∵∠DOA+∠2=90°,∠2+∠4=90°,
∴∠DOA=∠4,
∵∠DAB=∠ABC,
∴△AOD∽△BCO,
故选项④正确;
故答案为:①②④.
点评 本题考查了切线长定理和相似三角形的性质及判定,证明一条线段等于两条线段的和时,把一条线段分成两条线段,分别与两条线段对应相等得出;证明乘积式时,先化成比例式,证明所在的三角形相似.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 销售方式 | 粗加工后销售 | 精加工后销售 |
| 每吨获利(元) | 1000 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 矩形ABCD中,AC是对角线,AB=$\sqrt{3}$,将△ABC绕点C顺时针旋转60°,点B恰好落在AD边上的点E处,点A经过的路径是$\widehat{AF}$,则图中影阴部分的面积为$\frac{7}{6}π$-$\frac{3}{2}\sqrt{3}$.(结果保留π).
矩形ABCD中,AC是对角线,AB=$\sqrt{3}$,将△ABC绕点C顺时针旋转60°,点B恰好落在AD边上的点E处,点A经过的路径是$\widehat{AF}$,则图中影阴部分的面积为$\frac{7}{6}π$-$\frac{3}{2}\sqrt{3}$.(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
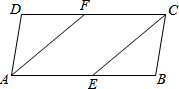 如图,在平行四边形ABCD中,已知AF平分∠DAB,CE平分∠BCD,
如图,在平行四边形ABCD中,已知AF平分∠DAB,CE平分∠BCD,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com