
分析 由抛物线的一般形式可知:a=-1,由对称轴方程x=-$\frac{b}{2a}$,可得一个等式-$\frac{b}{2×(-1)}$=-1,可解得b=-2,然后将点(2,-1)代入y=-x2-2x+c即可得到c,可得解析式.
解答 解:∵二次函数y=-x2+bx+c图象的对称轴是直线x=-1,
∴a=-1,$-\frac{b}{2a}$=-1,
∴-$\frac{b}{2×(-1)}$=-1,
解得,b=-2,
∵二次函数y=-x2+bx+c图象经过点(2,-1),
∴-1=-22-2×2+c
解得,c=7,
∴二次函数的表达式为:y=-x2-2x+7.
点评 此题考查了用待定系数法求二次函数的解析式,解题的关键是:熟练掌握待定系数法及对称轴表达式x=-$\frac{b}{2a}$.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
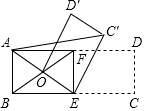 如图,已知点E、F是矩形ABCD的边BC、AD的中点,联结EF,将四边形ECDF绕点E逆时针旋转,点F正好与四边形ABEF对角线的交点O重合,得四边形OEC′D′,联结AC′,若AB=1,讨求线段AC′的长.
如图,已知点E、F是矩形ABCD的边BC、AD的中点,联结EF,将四边形ECDF绕点E逆时针旋转,点F正好与四边形ABEF对角线的交点O重合,得四边形OEC′D′,联结AC′,若AB=1,讨求线段AC′的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com