
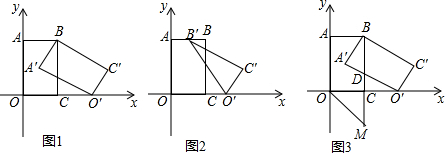
���� ��1�����ݵ������������ߺ�һ�Լ�ȫ�������ε����ʼ��ɽ�����⣮
��2�����������Σ�����ͼ2�У���0��t��1ʱ���ص������ǡ�MNB�䣬����ͼ3�У���1��t$��\frac{3}{2}$ʱ���ص������������MNHGO�䣬����ͼ4�У���$\frac{3}{2}$��t��2ʱ���ص��������ı���MNC��O�䣬����ͼ5�У���2��t��$\frac{5}{2}$ʱ���ص������ǡ�MNC�䣬�ֱ���⼴�ɣ�
��3���������������ۼ�����ͼ6�У��ٵ���POM=90��ʱ���ڵ���OMP��=90��ʱ��
��� �⣺��1��������OB��O��B��
��OB=O��B��
���ı���OABC���Σ�
��BC��OC��
��CO=CO�䣬
��B�����꣨1��$\sqrt{3}$����
��OC=1��
��O��C=1��
��O�䣨2��0����
����ͼ1�У���O��DB�ǵ��������Σ�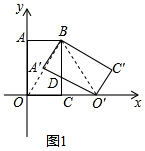
�����ǣ��ߡ�A��=��BCO��=90�㣬��A��DB=��CDO�䣬A��B=O��C��
���BA��D�ա�O��CD��
��BD=DO�䣬
���O��DB�ǵ��������Σ�
�ʴ�Ϊ��2��0�������������Σ�
��2������ͼ2�У���0��t��1ʱ���ص������ǡ�MNB�䣬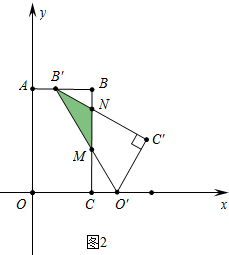
S=$\frac{1}{2}$��$\frac{2\sqrt{3}}{3}$t•t=$\frac{\sqrt{3}}{3}$t2��
����ͼ3�У���1��t$��\frac{3}{2}$ʱ���ص������������MNHGO�䣬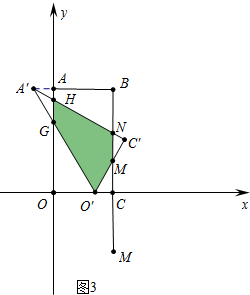
S=S��A��O��C��-S��A��GH-S��MNC��=$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$��2��$\frac{\sqrt{3}}{3}$��t-1��2-$\frac{1}{2}$��[1-2��t-2��]��$\frac{\sqrt{3}}{3}$[1-2��t-2��]=-$\sqrt{3}$t2+4$\sqrt{3}$t-4$\sqrt{3}$��
����ͼ4�У���$\frac{3}{2}$��t��2ʱ���ص��������ı���MNC��O�䣬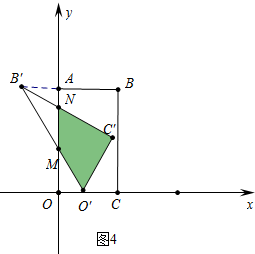
S=S��O��B��C��-S��MNB��=$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$��2��$\frac{\sqrt{3}}{3}$��t-1��2=-$\frac{\sqrt{3}}{3}$t2+$\frac{2\sqrt{3}}{3}$t+$\frac{\sqrt{3}}{6}$��
����ͼ5�У���2��t��$\frac{5}{2}$ʱ���ص������ǡ�MNC�䣬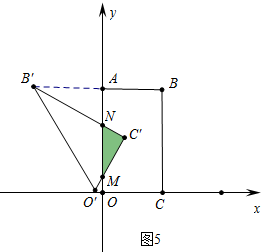
S=$\frac{1}{2}$��[1-2��t-2��]��$\frac{\sqrt{3}}{3}$[1-2��t-2��]=$\frac{2\sqrt{3}}{3}$t2-$\frac{10\sqrt{3}}{3}$t+$\frac{25\sqrt{3}}{6}$��
��������S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{3}{t}^{2}}&{��0��t��1��}\\{-\sqrt{3}{t}^{2}+4\sqrt{3}t-4\sqrt{3}}&{��1��t��\frac{3}{2}��}\\{-\frac{\sqrt{3}}{3}{t}^{2}+\frac{2\sqrt{3}}{3}t+\frac{\sqrt{3}}{6}}&{��\frac{3}{2}��t��2��}\\{\frac{2\sqrt{3}}{2}{t}^{2}-\frac{1=\sqrt{3}}{3}t+\frac{25\sqrt{3}}{6}}&{��2��t��\frac{5}{2}��}\end{array}\right.$��
��3����ͼ6�У����ڣ�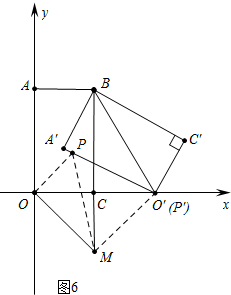
�ٵ���POM=90��ʱ����OC=CM=1��
���COM=45��=��POC��
��ֱ��OP����ʽΪy=x��
��ֱ��OA�Ľ���ʽΪy=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$��
��$\left\{\begin{array}{l}{y=x}\\{y=-\frac{\sqrt{3}}{3}x+\frac{2\sqrt{3}}{3}}\end{array}\right.$���$\left\{\begin{array}{l}{x=\sqrt{3}-1}\\{y=\sqrt{3}-1}\end{array}\right.$��
���P������$\sqrt{3}$-1��$\sqrt{3}$-1����
�ڵ���OMP��=90��ʱ����֪P����O���غϣ�
��ʱ��P�����꣨2��0����
����������P������2��0����$\sqrt{3}$-1��$\sqrt{3}$-1����
���� ���⿼���ı����ۺ��⡢ȫ�������ε��ж������ʡ�һ�κ��������ε����ʡ����������ε����ʵ�֪ʶ������Ĺؼ���ѧ�ử��ͼ�Σ�ѧ��������ۣ�ע���Ա�����ȡֵ��Χ������©�⣬�����п�ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
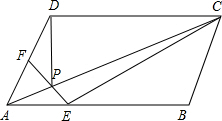 ��֪ƽ���ı���ABCD�У�E��F�ֱ���AB��AD�ϵĵ㣬EF��Խ���AC����P����$\frac{AE}{EB}$=$\frac{1}{2}$��$\frac{AF}{FD}$=$\frac{2}{3}$����$\frac{{S}_{��PAD}}{{S}_{��PCE}}$��ֵΪ��������
��֪ƽ���ı���ABCD�У�E��F�ֱ���AB��AD�ϵĵ㣬EF��Խ���AC����P����$\frac{AE}{EB}$=$\frac{1}{2}$��$\frac{AF}{FD}$=$\frac{2}{3}$����$\frac{{S}_{��PAD}}{{S}_{��PCE}}$��ֵΪ��������| A�� | $\frac{3}{7}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{18}{13}$ | D�� | $\frac{18}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com