
【题目】已知△ABC,AB=AC=5,BC=8,∠PDQ的顶点D在BC边上,DP交AB边于点E,DQ交AB边于点O且交CA的延长线于点F(点F与点A不重合),设∠PDQ=∠B,BD=3.
(1)求证:△BDE∽△CFD;
(2)设BE=x,OA=y,求y关于x的函数关系式,并写出定义域;
(3)当△AOF是等腰三角形时,求BE的长.
【答案】
(1)
解:∵AB=AC,
∴∠B=∠C,
∵∠EDC=∠B+∠BED,
∴∠FDC+∠EDO=∠B+∠BED,
∵∠EDO=∠B,
∴∠BED=∠EDC,
∵∠B=∠C,
∴△BDE∽△CFD
(2)
解:过点D作DM∥AB交AC于M(如图1中).

∵△BDE∽△CFD,
∴ ![]() ,∵BC=8,BD=3,BE=x,
,∵BC=8,BD=3,BE=x,
∴ ![]() ,
,
∴FC= ![]() ,
,
∵DM∥AB,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴DM= ![]() ,
,
∵DM∥AB,
∴∠B=∠MDC,
∴∠MDC=∠C,
∴CM=DM= ![]() ,FM=
,FM= ![]() ﹣
﹣ ![]() ,
,
∵DM∥AB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴y= ![]() (0<x<3)
(0<x<3)
(3)
解:①当AO=AF时,
由(2)可知AO=y= ![]() ,AF=FC﹣AC=
,AF=FC﹣AC= ![]() ﹣5,
﹣5,
∴ ![]() =
= ![]() ﹣5,解得x=
﹣5,解得x= ![]() .
.
∴BE= ![]()
②当FO=FA时,易知DO=AM= ![]() ,作DH⊥AB于H(如图2中),
,作DH⊥AB于H(如图2中),
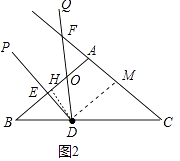
BH=BDcos∠B=3× ![]() =
= ![]() ,
,
DH=BDsin∠B=3× ![]() =
= ![]() ,
,
∴HO= ![]() =
= ![]() ,
,
∴OA=AB﹣BH﹣HO= ![]() ,
,
由(2)可知y= ![]() ,即
,即 ![]() =
= ![]() ,解得x=
,解得x= ![]() ,
,
∴BE= ![]() .
.
③当OA=OF时,设DP与CA的延长线交于点N(如图3中).

∴∠OAF=∠OFA,∠B=∠C=∠ANE,
由△ABC≌△CDN,可得CN=BC=8,ND=5,
由△BDE≌△NAE,可得NE=BE=x,ED=5﹣x,
作EG⊥BC于G,则BG= ![]() x,EG=
x,EG= ![]() x,
x,
∴GD= ![]() ,
,
∴BG+GD= ![]() x+
x+ ![]() =3,
=3,
∴x= ![]() >3(舍弃),
>3(舍弃),
综上所述,当△OAF是等腰三角形时,BE= ![]() 或
或 ![]()
【解析】(1)根据两角对应相等两三角形相似即可证明.(2)过点D作DM∥AB交AC于M(如图1中).由△BDE∽△CFD,得 ![]() ,推出FC=
,推出FC= ![]() ,由DM∥AB,得
,由DM∥AB,得 ![]() ,推出DM=
,推出DM= ![]() ,由DM∥AB,推出∠B=∠MDC,∠MDC=∠C,CM=DM=
,由DM∥AB,推出∠B=∠MDC,∠MDC=∠C,CM=DM= ![]() ,FM=
,FM= ![]() ﹣
﹣ ![]() ,于DM∥AB,得
,于DM∥AB,得 ![]() ,代入化简即可.(3)分三种情形讨论①当AO=AF时,②当FO=FA时,③当OA=OF时,分别计算即可.
,代入化简即可.(3)分三种情形讨论①当AO=AF时,②当FO=FA时,③当OA=OF时,分别计算即可.


科目:初中数学 来源: 题型:
【题目】在数轴上,O表示原点,A、B两点分别表示﹣8和2.
(1)求出线段AB的长度;
(2)动点P从A出发沿数轴向右运动,速度为每秒5个单位长度;同时点Q从B出发,沿数轴向右运动,速度为每秒3个单位长度,当P、Q重合时,两点同时停止运动.设两点运动时间为t秒,用含有t的式子表示线段PQ的长;
(3)在(2)的条件下,t为何值时,点P、点Q到原点O的距离相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“626国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作如表频数分布表和频数分布直方图,请根据图表提供的信息,解答下列问题:
少分数段(x表示分数) | 频数 | 频率 |
50≤x<60 | 4 | 0.1 |
60≤x<70 | a | 0.2 |
70≤x<80 | 12 | b |
80≤x<90 | 10 | 0.25 |
90≤x<100 | 6 | 0.15 |

(1)表中a= , b= , 并补全直方图
(2)若用扇形统计图描述此成绩分布情况,则分数段80≤x<100对应扇形的圆心角度数是;
(3)请估计该年级分数在60≤x<100的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知,在△ABC中,∠ACB=90°,AC=BC,点D是AB边上的中点,点M和点N是动点,分别从A,C出发,以相同的速度沿AC,CB边上运动.
(1)判断DM与DN的关系,并说明理由;
(2)若AC=BC=2,请直接写出四边形MCND的面积;
(3)如图②,当点M运动到C点后,将改变方向沿着CB运动,此时,点N在CB延长线上,过M作ME⊥CD于点E,过点N作NF⊥DB交DB延长线于F,求证:ME=NF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,拦水坝的横断面为梯形ABCD,AB∥CD,坝顶宽DC为6米,坝高DG为2米,迎水坡BC的坡角为30°,坝底宽AB为(8+2 ![]() )米.
)米. 
(1)求背水坡AD的坡度;
(2)为了加固拦水坝,需将水坝加高2米,并且保持坝顶宽度不变,迎水坡和背水坡的坡度也不变,求加高后坝底HB的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”,鼓楼区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中某些家庭一年的月平均用水量(单位:吨),调查中发现,每户用水量每月均在10﹣14吨范围,并将调查结果制成了如图所示的条形统计图(不完整)和扇形统计图.

(1)请将条形统计图补充完整;
(2)这些家庭月用水量数据的平均数是 ,众数是 ,中位数是 ;
(3)根据样本数据,估计鼓楼区直属机关300户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)连接DE,BF,若BD⊥EF,试探究四边形EBFD的形状,并对结论给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”小长假,小颖和小梅两家计划从“北京天安门”“三亚南山”“内蒙古大草原”三个景区中任意选择一景区游玩,小颖和小梅制作了如下三张质地大小完全相同的卡片,背面朝上洗匀后各自从中抽去一张来确定游玩景区(第一人抽完放回洗匀后另一人再抽去),则两人抽到同一景区的概率是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com