
如图是一个等腰直角三角形彩色纸,
AC=BC=40 cm,将斜边上的高CD四等分,然后裁出3张宽度相等的长方形纸条.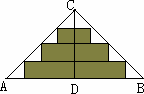
(1)分别求出这3张长方形纸条的长度;
(2)若用这些纸条为一幅正方形美术作品镶边(纸条不重叠),如图,正方形美术作品的面积最大不能超过多少cm?

|
解: (1)在Rt△ABC中,AC=BC=40 cm,所以AB=因为 CD⊥AB,所以AD=BD=CD,所以CD=因为最上面正方形纸条的长是 所以这三张纸条的长依次是 10(2)因为3张长方形纸条连接在一起的总长度为10 所以给这幅美术作品所镶的边框,可以看作由 4张宽为5所以正方形的边长为 15所以这幅美术作品的面积最大不能超过 20 cm2. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
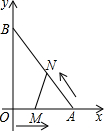 (2012•湛江)如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒
(2012•湛江)如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒| 5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 一个等腰直角三角形和一个正方形如图摆放,被分割成了①、②、③、④、⑤五个部分,如果①,②,③这三块的面积比依次为1:4:35,那么④,⑤这两块的面积比是
一个等腰直角三角形和一个正方形如图摆放,被分割成了①、②、③、④、⑤五个部分,如果①,②,③这三块的面积比依次为1:4:35,那么④,⑤这两块的面积比是查看答案和解析>>
科目:初中数学 来源: 题型:
 若不存在,请说明理由.
若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:三点一测丛书九年级数学上 题型:044
七巧板是我国古代人民创造的一种益智游戏,是由一个正方形、一个平行四边形和五个等腰直角三角形构成(如图),其中等腰直角三角形有三种不同尺寸.请你指出其中有哪几组全等图形.(用序号表示)

查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com