
分析 (1)待定系数法求解可得;
(2)根据题意得W总=y甲+y乙=$\frac{2}{5}$(10-x2)+(-0.2x22+1.6x2)=-0.2x22+1.2x2+4=-0.2(x2-3)2+5.8,据此可得.
解答 解:(1)将x=5、y=2代入y甲=kx1,得:5k=2,
解得:k=$\frac{2}{5}$,
∴y甲=$\frac{2}{5}$x1;
将x=2、y=2.4和x=4、y=3.2代入y乙=ax22+bx2,得:
$\left\{\begin{array}{l}{4a+2b=2.4}\\{16a+4b=3.2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-0.2}\\{b=1.6}\end{array}\right.$,
∴y乙=-0.2x22+1.6x2;
(2)根据题意得:W总=y甲+y乙
=$\frac{2}{5}$(10-x2)+(-0.2x22+1.6x2)
=-0.2x22+1.2x2+4
=-0.2(x2-3)2+5.8,
当x2=3时,W总利润最大为5.8万元,
答:当种植甲种树苗7亩,乙种树苗3亩时,所获利润最大,种植所获得的最大利润为5.8万元.
点评 本题主要考查二次函数的应用,熟练掌握待定系数法求函数解析式及销售问题中的最大利润问题是解题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1+\sqrt{21}}{2}$或$\frac{1-\sqrt{21}}{2}$ | B. | 6或-$\frac{9}{5}$ | ||
| C. | 6或$\frac{1-\sqrt{21}}{2}$ | D. | 6或-$\frac{9}{5}$或$\frac{1-\sqrt{21}}{2}$或$\frac{1+\sqrt{21}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
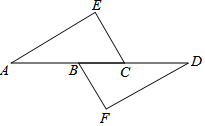 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com