
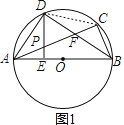
【题目】已知:如图,△ABC内接于⊙O,AB为直径,点D是弧AC上的一点,连接AD、BD,AC交BD于点F,DE⊥AB于点E,交AC于点P,∠ABD=∠CBD=∠CAD.
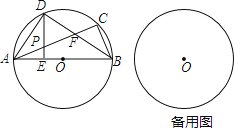
(1)求证:PA=PD;
(2)判断AP与PF是否相等,并说明理由;
(3)当点C为半圆弧的中点,小李通过操作发现BF=2AD,请问小李的发现是否正确?若正确,请说明理由;若不正确,请写出BF与AD正确的关系式.
【答案】(1)见解析;(2)相等,理由见解析;(3)小李的发现是正确的,理由见解析
【解析】
试题分析:(1)如图1,连接CD,由AB是半⊙O的直径,DE⊥AB于E,得到∠DBA+∠DAB=∠ADE+∠DAE=90°,于是得到∠DBA=∠ADE,根据圆周角定理得到∠DCA=∠DBA=∠DAC,即可求出结论;
(2)根据圆周角定理求出∠DAP=∠ADP,求出AP=DP,求出∠BDE=∠DAE,求出DP=FP,即可得出答案;
(3)根据全等三角形的性质和判定求出AD=BF,DA=DG,即可得出答案.
解:(1)如图1,连接CD,
∵AB是半⊙O的直径,
∴∠ADB=90°,
∵DE⊥AB于E,
∴∠DEA=90°,
∴∠DBA+∠DAB=∠ADE+∠DAE=90°,
∴∠DBA=∠ADE,
∵点D是弧AC的中点,
∴∠DCA=∠DBA=∠DAC,
∴∠DAP=∠ADP,
∴AP=DP;
(2)AP=PF;
理由是:∵AB是直径,DE⊥AB,
∴∠ADB=∠DEB=90°,
∴∠ADE=∠ABD,
∵D为弧AC中点,
∴∠DAC=∠DBA,
∴∠ADE=∠DAC,
∴AP=DP,∠FDE=∠AFD,
∴DP=PF,
∴AP=PF;
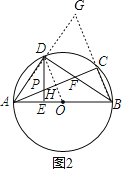
(3)小李的发现是正确的,
理由是:如图2,延长AD、BC,两线交于G,
∵C为半圆弧的中点,D是弧AC的中点,
∴∠CBD=∠GAC,∠BCA=∠ACG=90°,AC=BC,
在△CBF和△CAG中,
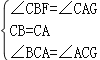 ,
,
∴△CBF≌△CAG(ASA),
∴BF=AG,
∵BC为直径
∴∠ADB=90°,
∵D为弧AC中点,
∴∠GBD=∠ABD
在△ADB和△GDB中,
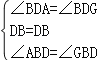 ,
,
∴△ADB≌△GDB(ASA),
∴DG=DA=![]() AG,
AG,
∴BF=2AD.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,正中设计一个圆形喷水池,若四周圆形和中间圆形的半径均为![]() 米,广场长为
米,广场长为![]() 米,宽为
米,宽为![]() 米.
米.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为500米,宽为300米,圆形花坛的半径为20米,求广场空地的面积(计算结果保留![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
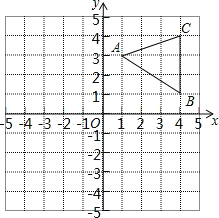
(1)请按要求画图:
①画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2.
(2)请写出直线B1C1与直线B2C2的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(.2016湖北随州第8题)随州市尚市“桃花节”观赏人数逐年增加,据有关部门统计,2014年约为20万人次,2016年约为28.8万人次,设观赏人数年均增长率为x,则下列方程中正确的是( )
A.20(1+2x)=28.8 B.28.8(1+x)2=20
C.20(1+x)2=28.8 D.20+20(1+x)+20(1+x)2=28.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com