
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

【答案】![]()
【解析】过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,如图所示.

∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥y轴,BE⊥y轴,
∴∠ACD+∠CAD=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,∠BCE=∠CAD.
在△ACD和△CBE中,由 ,
,
∴△ACD≌△CBE(ASA).
设点B的坐标为(m,﹣![]() )(m<0),则E(0,﹣
)(m<0),则E(0,﹣![]() ),点D(0,3﹣m),点A(﹣
),点D(0,3﹣m),点A(﹣![]() ﹣3,3﹣m),
﹣3,3﹣m),
∵点A(﹣![]() ﹣3,3﹣m)在反比例函数y=﹣
﹣3,3﹣m)在反比例函数y=﹣![]() 上,
上,
 ,解得:m=﹣3,m=2(舍去).
,解得:m=﹣3,m=2(舍去).
∴点A的坐标为(﹣1,6),点B的坐标为(﹣3,2),点F的坐标为(﹣1,2),
∴BF=2,AF=4,
![]()
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】在创建全国森林城市的活动中,我区一“青年突击队”决定义务整修一条1000米长的绿化带,开工后,附近居民主动参加到义务劳动中,使整修的速度比原计划提高了一倍,结果提前4小时完成任务,问“青年突击队”原计划每小时整修多少米长的绿化带?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:

请结合图表完成下列各题:
(1)①表中a的值为 ; ②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
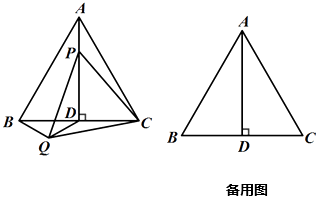
【题目】如图,正△ABC 中,高线 ![]() ,点
,点 ![]() 从点
从点 ![]() 出发,沿着
出发,沿着 ![]() 运动到点
运动到点 ![]() 停止,以
停止,以 ![]() 为边向左下方作正
为边向左下方作正 ![]() ,连接
,连接 ![]() ,
, ![]() .
.
(1)求证: ![]() ≌
≌ ![]() ;
;
(2)在点P的运动过程中,当 ![]() 是等腰三角形时,求
是等腰三角形时,求 ![]() 的度数;
的度数;
(3)直接写出在点 P的运动过程中, ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:三角形三条内角平分线的交点叫做三角形的内心;
性质:内心到三角形三边的距离相等.
如图1,点 ![]() 为
为 ![]() 的内心,
的内心, ![]() 于
于 ![]() ,
, ![]() 于E,
于E, ![]() 于
于 ![]() ,则有
,则有 ![]() .
.
问题:如何求 ![]() 的值呢?
的值呢?
探究:
(1)小明思路:设△ABC的面积为 ![]() ,
, ![]() 的面积为
的面积为 ![]() ,
, ![]() 的面积为
的面积为 ![]() ,
, ![]() 的面积为
的面积为 ![]() ,利用
,利用 ![]() 可求
可求 ![]() .
.
①图1中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,请你根据小明的思路求出
,请你根据小明的思路求出 ![]() 的值;
的值;
②如图2,△ABC中, ![]() ,设
,设 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为 △ABC的内心,
为 △ABC的内心, ![]() 于
于 ![]() ,
, ![]() 于E,
于E, ![]() 于
于 ![]() .若设
.若设 ![]() ,请用含
,请用含 ![]() ,
, ![]() ,
, ![]() 的式子表示
的式子表示 ![]() ;
;
(2)小亮思路:“凡角平分处,必有轴对称”. 如图2,易得: ![]() ,
, ![]() ,
, ![]() . 请你根据小亮的思路,用含
. 请你根据小亮的思路,用含 ![]() ,
, ![]() ,
, ![]() 的式子表示
的式子表示 ![]() ;
;
(3)①根据上述所列两式,求证: ![]() ;
;
②应用:已知一个直角三角形的两直角边长分别为 ![]() 和
和 ![]() ,求该三角形的内心到任意一边的距离
,求该三角形的内心到任意一边的距离 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班要从甲、乙两名同学中选拔出一人,代表班级参加学校的一分钟踢毽子体能素质比赛,在一段时间内的相同条件下,甲、乙两人进行了六场一分钟踢毽子的选拔测试,根据他们的成绩绘制出如图的统计表和不完整的折线统计图.
甲、乙两人选拔测试成绩统计表
甲成绩 | 乙成绩 | |
第1场 | 87 | 87 |
第2场 | 94 | 98 |
第3场 | 91 | 87 |
第4场 | 85 | 89 |
第5场 | 91 | 100 |
第6场 | 92 | 85 |
中位数 | 91 | n |
平均数 | m | 91 |
并计算出乙同学六场选拔测试成绩的方差:
S乙2= ![]() =
= ![]()

(1)m= , n= , 并补全全图中甲、乙两人选拔测试成绩折线统计图;
(2)求甲同学六场选拔测试成绩的方差S甲2;
(3)分别从平均数、中位数和方差的角度分析比较甲、乙二人的成绩各有什么特点?
(4)经查阅该校以往本项比赛的资料可知,①成绩若达到90次/min,就有可能夺得冠军,你认为选谁参赛更有把握夺冠?为什么?
②该项成绩的最好记录是95次/min,就有可能夺得冠军,你认为选谁参赛更有把握夺冠?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com