
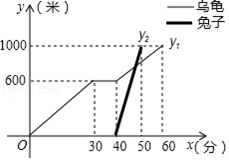
 “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:分析 ①由兔子出发时的时间为40分可得出①错误;②观察函数图象即可得出“龟兔再次赛跑”的路程为1000米,即②正确;③用40-30即可得出乌龟在途中休息了10分钟,即③正确;④设y2=k2x+b2(k2≠0),在40≤x≤60时间段内y1=k1x+b1(k1≠0),观察函数图象找出点的坐标利用待定系数法即可求出两函数关系式,令y1=y2求出x值,再将其代入y1中即可得出兔子在途中750米处追上乌龟,即④正确.综上即可得出结论.
解答 解:观察函数图象可得出:
①兔子出发的时间为40分,①错误;
②“龟兔再次赛跑”的路程为1000米,②正确;
③乌龟休息的时间为40-30=10(分钟),③正确;
④设y2=k2x+b2(k2≠0),在40≤x≤60时间段内y1=k1x+b1(k1≠0),
将(40,600)、(60,1000)代入y1=k1x+b1中,得:
$\left\{\begin{array}{l}{600=40{k}_{1}+{b}_{1}}\\{1000=60{k}_{1}+{b}_{1}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{1}=20}\\{{b}_{1}=-200}\end{array}\right.$,
∴y1=20x-200(40≤x≤60).
同理可求出:y2=100x-4000(40≤x≤50).
令y1=y2,即20x-200=100x-4000,
解得:x=$\frac{95}{2}$,
∴y1=20x-200=20×$\frac{95}{2}$-200=750,
∴兔子在途中750米处追上乌龟,④正确.
故答案为:②③④.
点评 本题考查了一次函数的应用以及待定系数法求一次函数解析式,观察函数图象找出点的坐标再利用待定系数法求出函数解析式是解题的关键.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在河岸L的同侧有A、B两村,现拟在河岸边修建一座水泵站P,要求使管道PA、PB所用的水管最短,另修一码头Q,要求码头到A、B两村的距离相等,试画出P、Q所在的位置.
在河岸L的同侧有A、B两村,现拟在河岸边修建一座水泵站P,要求使管道PA、PB所用的水管最短,另修一码头Q,要求码头到A、B两村的距离相等,试画出P、Q所在的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com