
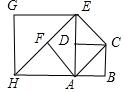
 如图,在边长为1的正方形ABCD中,连结对角线AC,以AC为边作第二个正方形,连结对角线AE,以AE为边作第三个正方形…按此规律所作的第2017个正方形的边长是( )
如图,在边长为1的正方形ABCD中,连结对角线AC,以AC为边作第二个正方形,连结对角线AE,以AE为边作第三个正方形…按此规律所作的第2017个正方形的边长是( )| A. | 22016 | B. | 22016$\sqrt{2}$ | C. | 21008 | D. | 21008$\sqrt{2}$ |
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
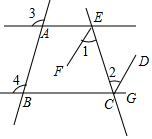 已知:如图,直线AE,BC被直线AB,EC所截,已知∠3=∠4,EF平分∠AEC,CD平分∠ECG,将下列证明EF∥CD的过程及理由填写完整.
已知:如图,直线AE,BC被直线AB,EC所截,已知∠3=∠4,EF平分∠AEC,CD平分∠ECG,将下列证明EF∥CD的过程及理由填写完整.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
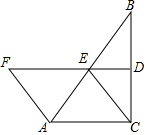 如图,∠ACB=90°,D,E分别为BC,AB的中点,DE的延长线交AF于F,∠F=∠FEA.
如图,∠ACB=90°,D,E分别为BC,AB的中点,DE的延长线交AF于F,∠F=∠FEA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 板房型号 | 所需板材 | 安置人数 |
| A型板房 | 54m2 | 5 |
| B型板房 | 78m2 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com