
【题目】下表是二次函数y=ax2+bx+c的部分x,y的对应值:
x | … | -1 | - | 0 |
| 1 |
| 2 |
| 3 | … |
y | … | 2 |
| -1 | - | -2 | - | -1 |
| 2 | … |
(1)此二次函数图象的顶点坐标是 ;
(2)当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是 。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:
(1)观察、分析表格中的数据可知,当x=0和x=2时,y的值都是-1,由此可确定该二次函数的图象关于直线x=1对称,而当x=1时,y=-2,由此可得抛物线的顶点坐标为(1,-2);
(2)由抛物线的顶点(1,-2)在直线y=x+n的下方可得,在y=x+n中,当x=1时,y>-2,由此可得:1+n>-2,解此不等式即可得到n的取值范围.
试题解析:
(1)观察、分析表格中的数据可知,当x=0和x=2时,y的值都是-1,
∴二次函数y=ax2+bx+c的对称轴为直线:x=1,
∵当x=1时,y=-2,
∴二次函数y=ax2+bx+c的顶点坐标为(1,-2);
(2)∵抛物线y=ax2+bx+c的顶点(1,-2)在直线y=x+n的下方,
∴在y=x+n中,当x=1时,y>-2,由此可得:1+n>-2,解得n>-3,
∴n的取值范围为:n>-3.


科目:初中数学 来源: 题型:
【题目】已知坐标平面内的点A(3,2),B(1,3),C(﹣1,﹣6),D(2a,4a﹣4)中只有一点不在直线l上,则这一点是( )
A.点AB.点BC.点CD.点D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
(1)证明:△ABM∽△MCN;
(2)若△ABM的周长与△MCN周长之比是4:3,求NC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
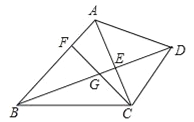
【题目】已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GEGD.
(1)求证:∠ACF=∠ABD;
(2)连接EF,求证:EFCG=EGCB.
查看答案和解析>>
科目:初中数学 来源: 题型:
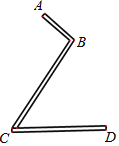
【题目】现有一个“![]() ”型的工件(工件厚度忽略不计),如图示,其中
”型的工件(工件厚度忽略不计),如图示,其中![]() 为20
为20![]() ,
,![]() 为60
为60![]() ,
,![]() ,
,![]() ,求该工件如图摆放时的高度(即
,求该工件如图摆放时的高度(即![]() 到
到![]() 的距离).
的距离).
(结果精确到0.1![]() ,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
查看答案和解析>>
科目:初中数学 来源: 题型:
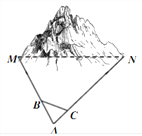
【题目】中国高铁近年来用震惊世界的速度不断发展,已成为当代中国一张耀眼的“国家名片”。修建高铁时常常要逢山开道、遇水搭桥。如图,某高铁在修建时需打通一直线隧道MN(M、N为山的两侧),工程人员为了计算MN两点之间的直线距离,选择了在测量点A、B、C进行测量,点B、C分别在AM、AN上,现测得AM=1200米,AN=2000米,AB=30米,BC=45米,AC=18米,求直线隧道MN的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)若![]() ,作
,作![]() ,点
,点![]() 在
在![]() 内.
内.
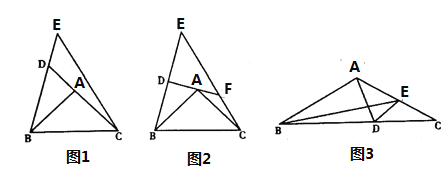
①如图1,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的度数为 ;
的度数为 ;
②如图2,![]() 垂直平分
垂直平分![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,求
,求![]() 的值;
的值;
(2)如图3,若![]() ,点
,点![]() 在
在![]() 边上,
边上,![]() ,点
,点![]() 在
在![]() 边上,连接
边上,连接![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点的坐标为(﹣1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐 标为(3,﹣1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件,使△ABC ≌ △DEC,则添加的条件不能为( )
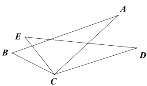
A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com