
ЁОЬтФПЁПЛЭММЦЫуЃК
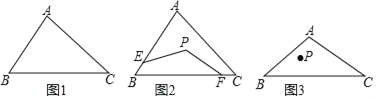
(1)вбжЊЁїABCЃЌЧыгУГпЙцдкЭМ1жаЁїABCФкШЗЖЈвЛИіЕуPЃЌЪЙЕУЕуPЕНABКЭBCЕФОрРыЯрЕШЃЌЧвТњзуPЕНЕуBКЭЕуCЕФОрРыЯрЕШ(ВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃ)ЃЎ
(2)ШчЭМ2ЃЌШчЙћЕуPЪЧ(1)жаЧѓзїЕФЕуЃЌЕуEЁЂFЗжБ№дкБпABЁЂBCЩЯЃЌЧвPEЃНPFЃЎ
ЂйШєЁЯABCЃН60ЁуЃЌЧѓЁЯEPFЕФЖШЪ§ЃЛ
ЂкШєBEЃН2ЃЌBFЃН8ЃЌEPЃН5ЃЌЧѓBPЕФГЄЃЎ
(3)ШчЭМ3ЃЌШчЙћЕуPЪЧЁїABCФквЛЕуЃЌЧвЕуPЕНЕуBЕФОрРыЪЧ7ЃЌШєЁЯABCЃН45ЁуЃЌЧыЗжБ№дкABЁЂBCЩЯЧѓзїСНИіЕуMЁЂNЃЌЪЙЕУЁїPMNЕФжмГЄзюаЁ(ВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃ)ЃЌдђЁїPMNЕФзюаЁжЕЮЊ______.
ЁОД№АИЁП(1)МћНтЮіЃЛ(2)ЂйЁЯEPFЃН120ЁуЃЛЂкBPЃН![]() ЃЛ(3)7
ЃЛ(3)7![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉзїЁЯABCЕФЦНЗжЯпBMЃЌЯпЖЮBCЕФДЙжБЦНЗжЯпEFЃЌжБЯпEFНЛЩфЯпBMгкЕуPЃЌЕуPМДЮЊЫљЧѓЃЛ
ЃЈ2ЃЉЂйгЩRtЁїPMEЁеRtЁїPNFЃЈHLЃЉЃЌЭЦГіЁЯEPM=ЁЯFPNЃЌЭЦГіЁЯEPF=ЁЯMPNЃЌМДПЩНтОіЮЪЬтЃЛ
ЂкгЩRtЁїPMBЁеRtЁїPNBЃЈHLЃЉЃЌЭЦГіBM=BNЃЌгЩRtЁїPMEЁеRtЁїPNFЃЈHLЃЉЃЌЭЦГіEM=FNЃЌЭЦГіBE+BF=BM-EM+BN+NF=2BN=10ЃЌЭЦГіBN=NM=5ЃЌдйРћгУЙДЙЩЖЈРэМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЗжБ№зїЕуPЙигкБпABЁЂBCЕФЖдГЦЕуEЁЂFЃЌСЌНгEFЃЌЗжБ№гыБпABЁЂBCНЛгкЕуMЁЂNЃЌСЌНгPMЁЂPNЃЎдђЯпЖЮEFЕФГЄЖШМДЮЊЁїPMNЕФжмГЄЕФзюаЁжЕЃЛ
НтЃК(1)ШчЭМЃЌЕуPМДЮЊЫљЧѓЃЛ
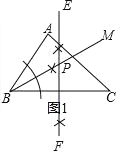
(2)ЂйСЌНгBPЃЌзїPMЁЭABгкMЃЌPNЁЭBCгкNЃЎ
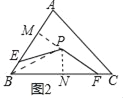
ЁпBPЦНЗжЁЯABCЃЌPMЁЭABЃЌPNЁЭBCЃЌ
ЁрPMЃНPNЃЌ
ЁпPEЃНPFЃЌЁЯPMEЃНЁЯPNFЃН90ЁуЃЌ
ЁрRtЁїPMEЁеRtЁїPNF(HL)ЃЌ
ЁрЁЯEPMЃНЁЯFPNЃЌ
ЁрЁЯEPFЃНЁЯMPNЃЌ
ЁпЁЯMPNЃН360ЁуЉ90ЁуЉ90ЁуЉ60ЁуЃН120ЁуЃЌ
ЁрЁЯEPFЃН120ЁуЃЎ
ЂкЁпPBЃНPBЃЌPMЃНPNЃЌЁЯPMBЃНЁЯPFBЃН90Ёу
ЁрRtЁїPMBЁеRtЁїPNB(HL)ЃЌ
ЁрBMЃНBNЃЌ
ЁпRtЁїPMEЁеRtЁїPNF(HL)ЃЌ
ЁрEMЃНFNЃЌ
ЁрBE+BFЃНBMЉEM+BN+NFЃН2BNЃН10ЃЌ
ЁрBNЃНNMЃН5ЃЌ
ЁпBEЃН2ЃЌPEЃН5ЃЌ
ЁрEMЃН3ЃЌPMЃН![]() ЃН4ЃЌ
ЃН4ЃЌ
ЁрBPЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ
(3)ЗжБ№зїЕуPЙигкБпABЁЂBCЕФЖдГЦЕуEЁЂFЃЌСЌНгEFЃЌЗжБ№гыБпABЁЂBCНЛгкЕуMЁЂNЃЌСЌНгPMЁЂPNЃЎдђЯпЖЮEFЕФГЄЖШМДЮЊЁїPMNЕФжмГЄЕФзюаЁжЕЃЎ
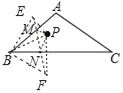
ЁпЕуEгыЕуPЙигкABЖдГЦЃЌЕуFгыЕуPЙигкBCЖдГЦЃЌ
ЁрЁЯEBAЃНЁЯPBAЃЌЁЯFBCЃНЁЯPBCЃЌBEЃНBFЃНBPЃН7ЃЎ
ЁрEFЃН![]() BEЃН7
BEЃН7![]()
ЁрЁїPMNжмГЄЕФзюаЁжЕЮЊ7![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊ7![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌЁЯB=90ЁуЃЌABЁЮED ,НЛBCгкEЃЌНЛ ACгкFЃЌ DE = BC,![]() .
.

ЃЈ1ЃЉ ЧѓжЄЃКЁїFCD ЪЧЕШбќШ§НЧаЮ
ЃЈ2ЃЉ ШєAB=3.5cm,ЧѓCDЕФГЄЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫГДЮСЌНсЖдНЧЯпЯрЕШЕФЫФБпаЮЕФЫФБпжаЕуЫљЕУЭМаЮЪЧЃЈ ЃЉ
A.е§ЗНаЮ
B.ОиаЮ
C.СтаЮ
D.вдЩЯЖМВЛЖд
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯB=30ЁуЃЌвдAЮЊдВаФЃЌШЮвтГЄЮЊАыОЖЛЛЁЗжБ№НЛABЁЂACгкЕуMКЭNЃЌдйЗжБ№вдMЁЂNЮЊдВаФЃЌДѓгк![]() MNЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуPЃЌСЌНсAPВЂбгГЄНЛBCгкЕуDЃЌдђЯТСаЫЕЗЈжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ.
MNЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуPЃЌСЌНсAPВЂбгГЄНЛBCгкЕуDЃЌдђЯТСаЫЕЗЈжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ.
ЂйзїГіADЕФвРОнЪЧSASЃЛЂкЁЯADC=60Ёу
ЂлЕуDдкABЕФжаДЙЯпЩЯЃЛЂмSЁїDACЃКSЁїABD=1ЃК2ЃЎ

A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋЁїAB CбиDEЃЌEFЗелЃЌЖЅЕуAЃЌBОљТфдкЕуOДІЃЌЧвEAгыEBжиКЯгкЯпЖЮEOЃЌШєЁЯCDO+ЁЯCFO=98ЁуЃЌдђЁЯCЕФЖШЪ§ЮЊЃЈ ЃЉ
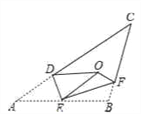
A. 40Ёу B. 41Ёу C. 42Ёу D. 43Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпl1ЁЮl2ЃЌжБЯпl3КЭжБЯпl1ЁЂl2НЛгкЕуCКЭDЃЌЕуPЪЧжБЯпl3ЩЯвЛЖЏЕу
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуPдкЯпЖЮCDЩЯдЫЖЏЪБЃЌЁЯPACЃЌЁЯAPBЃЌЁЯPBDжЎМфДцдкЪВУДЪ§СПЙиЯЕЃПЧыФуВТЯыНсТлВЂЫЕУїРэгЩЃЎ
ЃЈ2ЃЉЕБЕуPдкCЁЂDСНЕуЕФЭтВрдЫЖЏЪБЃЈPЕу![]() гыЕуCЁЂDВЛжиКЯЃЌШчЭМ2КЭЭМ3ЃЉЃЌЩЯЪіЃЈ1ЃЉжаЕФНсТлЪЧЗёЛЙГЩСЂЃПШєВЛГЩСЂЃЌЧыжБНгаДГіЁЯPACЃЌЁЯAPBЃЌЁЯPBDжЎМфЕФЪ§СПЙиЯЕЃЌВЛБиаДРэгЩЃЎ
гыЕуCЁЂDВЛжиКЯЃЌШчЭМ2КЭЭМ3ЃЉЃЌЩЯЪіЃЈ1ЃЉжаЕФНсТлЪЧЗёЛЙГЩСЂЃПШєВЛГЩСЂЃЌЧыжБНгаДГіЁЯPACЃЌЁЯAPBЃЌЁЯPBDжЎМфЕФЪ§СПЙиЯЕЃЌВЛБиаДРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСгыМЦЫуЃКЧыдФЖСвдЯТВФСЯЃЌВЂЭъГЩЯргІЕФШЮЮёЃЎ
ьГВЈФЧЦѕЃЈдМ1170Љ1250ЃЉЪЧвтДѓРћЪ§бЇМвЃЌЫћбаОПСЫвЛСаЪ§ЃЌетСаЪ§ЗЧГЃЦцУюЃЌБЛГЦЮЊьГВЈФЧЦѕЪ§СаЃЈАДеевЛЖЈЫГађХХСазХЕФвЛСаЪ§ГЦЮЊЪ§СаЃЉЃЎКѓРДШЫУЧдкбаОПЫќЕФЙ§ГЬжаЃЌЗЂЯжСЫаэЖрвтЯыВЛЕНЕФНсЙћЃЌдкЪЕМЪЩњЛюжаЃЌКмЖрЛЈЖфЃЈШчУЗЛЈЁЂЗЩбрВнЁЂЭђЪйОеЕШЃЉЕФАъЪ§ЧЁЪЧьГВЈФЧЦѕЪ§СажаЕФЪ§ЃЎьГВЈФЧЦѕЪ§СаЛЙгаКмЖргаШЄЕФаджЪЃЌдкЪЕМЪЩњЛюжавВгаЙуЗКЕФгІгУЃЎьГВЈФЧЦѕЪ§СажаЕФЕкnИіЪ§ПЩвдгУ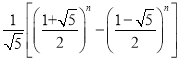 БэЪОЃЈЦфжаЃЌnЁн1ЃЉЃЎетЪЧгУЮоРэЪ§БэЪОгаРэЪ§ЕФвЛИіЗЖР§ЃЎ
БэЪОЃЈЦфжаЃЌnЁн1ЃЉЃЎетЪЧгУЮоРэЪ§БэЪОгаРэЪ§ЕФвЛИіЗЖР§ЃЎ

ШЮЮёЃКЧыИљОнвдЩЯВФСЯЃЌЭЈЙ§МЦЫуЧѓГіьГВЈФЧЦѕЪ§СажаЕФЕк1ИіЪ§КЭЕк2ИіЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЩШаЮAOBЕФдВаФНЧЮЊ124ЁуЃЌCЪЧ ![]() ЩЯвЛЕуЃЌдђЁЯACB=ЃЈ ЃЉ
ЩЯвЛЕуЃЌдђЁЯACB=ЃЈ ЃЉ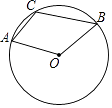
A.114Ёу
B.116Ёу
C.118Ёу
D.120Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЭЌвЛжБНЧзјБъЯЕжаЃЌКЏЪ§y=mx+mКЭy=Љmx2+2x+2ЃЈmЪЧГЃЪ§ЃЌЧвmЁй0ЃЉЕФЭМЯѓПЩФмЪЧЃЈ ЃЉ
A.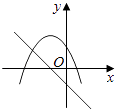
B.
C.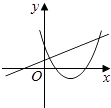
D.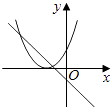
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com