
【题目】如图,在ABCD中,点E为AB的中点,F为BC上任意一点,把△BEF沿直线EF翻折,点B的对应点B′落在对角线AC上,则与∠FEB一定相等的角(不含∠FEB)有( )
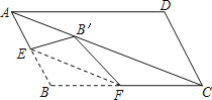
A.2个B.3个C.4个D.5个
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的![]() 位居民,得到这
位居民,得到这![]() 位居民一周内使用共享单车的次数分别为:
位居民一周内使用共享单车的次数分别为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)这组数据的中位数是________,众数是________;
(2)计算这![]() 位居民一周内使用共享单车的平均次数;
位居民一周内使用共享单车的平均次数;
(3)若该小区有![]() 名居民,试估计该小区居民一周内使用共享单车的总次数.
名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
画板的边长(dm) | 10 | 20 |
出售价(元/张) | 160 | 220 |
(1)求一张画板的出售价与边长之间满足的函数关系式;
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分12分)
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC = 8 cm,BC = 6 cm,EF = 9 cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).

解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校分别于2015年、2016年春季随机调查相同数量的学生,对学生做家务的情况进行调查(开展情况分为“基本不做”、“有时做”、“常常做”、“每天做”四种),绘制成部分统计图如下.
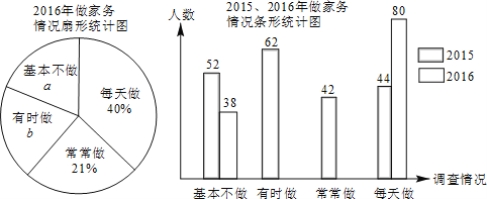
请根据图中信息,解答下列问题:
(1)a=______%,b=______%,“每天做”对应阴影的圆心角为______°;
(2)请你补全条形统计图;
(3)若该校2016年共有1200名学生,请你估计其中“每天做”家务的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
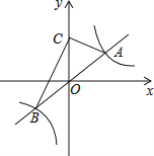
【题目】如图,反比例函数y=![]() (k>0)的图象与一次函数y=
(k>0)的图象与一次函数y=![]() x的图象交于A、B两点(点A在第一象限).
x的图象交于A、B两点(点A在第一象限).
(1)当点A的横坐标为4时.
①求k的值;
②根据反比例函数的图象,直接写出当-4<x<1(x≠0)时,y的取值范围;
(2)点C为y轴正半轴上一点,∠ACB=90°,且△ACB的面积为10,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com