练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，若BC=20厘米，BD=12厘米，则点D到AB的距离是（ ）
    A．7.5cm
    B．8cm
    C．12cm
    D．12.5cm
    【答案】分析：首先根据题意作图，然后过点D作DE⊥AB于E，由在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，即可得DE=CD，又由BC=20厘米，BD=12厘米，即可求得DE的长，即可得点D到AB的距离．
    解答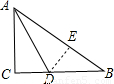：解：过点D作DE⊥AB于E，
    ∵在Rt△ABC中，∠C=90°，
    ∴CD⊥AC，
    ∵AD是∠BAC的平分线，
    ∴DE=CD，
    ∵BC=20厘米，BD=12厘米，
    ∴CD=BC-BD=8厘米，
    ∴DE=8厘米，
    即点D到AB的距离是8cm．
    故选B．
    点评：此题考查了角平分线的性质．此题比较简单，解题的关键是注意数形结合思想的应用，注意辅助线的作法．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网已知：如图，在Rt△ABC中，∠C=90°，AC=12，BC=9，D是AB上一点，以BD为直径的⊙O切AC于E，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，已知：在Rt△ABC中，∠C=90°，AB=12，点D是AB的中点，点O是△ABC的重心，则OD的长为（　　）
    A、12B、6C、2D、3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在Rt△ABC中，已知a及∠A，则斜边应为（　　）
    A、asinA
    B、
    a
    sinA
    C、acosA
    D、
    a
    cosA

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在Rt△ABC中，∠C=90°，CD⊥AB于D，CD：DB=1：3．求tanA和tanB．（要求画出图形）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，在Rt△ABC中，∠C=90°，CD⊥AB于D，且AD：BD=9：4，则AC：BC的值为（　　）
    A、9：4B、9：2C、3：4D、3：2

    查看答案和解析>>

    同步练习册答案