
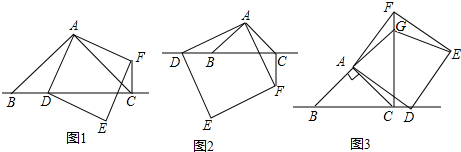
分析 (1)①根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论;②由正方形ADEF的性质可推出△DAB≌△FAC,根据全等三角形的性质得到CF=BD,∠ACF=∠ABD,根据余角的性质即可得到结论;
(2)根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质以及等腰直角三角形的角的性质可得到结论.
(3)根据等腰直角三角形的性质得到BC=$\sqrt{2}$AB=4,AH=$\frac{1}{2}$BC=2,求得DH=3,根据正方形的性质得到AD=DE,∠ADE=90°,根据矩形的性质得到NE=CM,EM=CN,由角的性质得到∠ADH=∠DEM,根据全等三角形的性质得到EM=DH=3,DM=AH=2,等量代换得到CN=EM=3,EN=CM=3,根据等腰直角三角形的性质得到CG=BC=4,根据勾股定理即可得到结论.
解答 解:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,$\left\{\begin{array}{l}{AD=AF}\\{∠BAD=∠CAF}\\{AB=AC}\end{array}\right.$,
∴△DAB≌△FAC,
∴∠B=∠ACF,
∴∠ACB+∠ACF=90°,即BC⊥CF;
故答案为:垂直;
②△DAB≌△FAC,
∴CF=BD,
∵BC=BD+CD,
∴BC=CF+CD;
故答案为:BC=CF+CD;
(2)CF⊥BC成立;BC=CD+CF不成立,CD=CF+BC.
∵正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,$\left\{\begin{array}{l}{AD=AF}\\{∠BAD=∠CAF}\\{AB=AC}\end{array}\right.$,
∴△DAB≌△FAC,
∴∠ABD=∠ACF,
∵∠BAC=90°,AB=AC,
∴∠ACB=∠ABC=45°.
∴∠ABD=180°-45°=135°,
∴∠BCF=∠ACF-∠ACB=135°-45°=90°,
∴CF⊥BC.
∵CD=DB+BC,DB=CF,
∴CD=CF+BC.
(3)解:过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,
∵∠BAC=90°,AB=AC,
∴BC=$\sqrt{2}$AB=4,AH=$\frac{1}{2}$BC=2,
∴CD=$\frac{1}{4}$BC=1,CH=$\frac{1}{2}$BC=2,
∴DH=3,
由(2)证得BC⊥CF,CF=BD=5,
∵四边形ADEF是正方形,
∴AD=DE,∠ADE=90°,
∵BC⊥CF,EM⊥BD,EN⊥CF,
∴四边形CMEN是矩形,
∴NE=CM,EM=CN,
∵∠AHD=∠ADE=∠EMD=90°,
∴∠ADH+∠EDM=∠EDM+∠DEM=90°,
∴∠ADH=∠DEM,
在△ADH与△DEM中,$\left\{\begin{array}{l}{∠ADH=∠DEM}\\{∠AHD=∠DME}\\{AD=DE}\end{array}\right.$,
∴△ADH≌△DEM,
∴EM=DH=3,DM=AH=2,
∴CN=EM=3,EN=CM=3,
∵∠ABC=45°,
∴∠BGC=45°,
∴△BCG是等腰直角三角形,
∴CG=BC=4,
∴GN=1,
∴EG=$\sqrt{G{N}^{2}+E{N}^{2}}$=$\sqrt{10}$.
点评 本题考查了全等三角形的判定和性质,正方形的性质,余角的性质,勾股定理,等腰直角三角形的判定和性质,矩形的判定和性质,正确地作出辅助线构造全等三角形是解题的关键.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:选择题
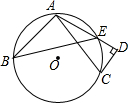 如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )
如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )| A. | $\frac{7}{12}$ | B. | $\frac{7}{24}$ | C. | $\frac{24}{25}$ | D. | $\frac{16}{25}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一艘轮船在诲面上由南向北航行,当它行驶到A处时,发现它的东北方向有一座灯塔B,轮船继续向北航行24海里后到达C处,发现灯塔B在它的北偏东75°方向,则此时轮船与灯塔B的距离是( )
如图,一艘轮船在诲面上由南向北航行,当它行驶到A处时,发现它的东北方向有一座灯塔B,轮船继续向北航行24海里后到达C处,发现灯塔B在它的北偏东75°方向,则此时轮船与灯塔B的距离是( )| A. | 24$\sqrt{2}$海里 | B. | 12$\sqrt{2}$海里 | C. | 24$\sqrt{3}$海里 | D. | 12$\sqrt{3}$海里 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
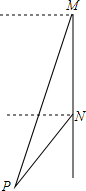 如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )
如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )| A. | 22.48 | B. | 41.68 | C. | 43.16 | D. | 55.63 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
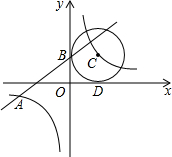 如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于点A(-4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=$\frac{4}{x}$的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于点A(-4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=$\frac{4}{x}$的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com