
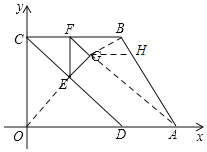
【题目】如图,四边形OABC的顶点A、C分别在x、y轴的正半抽上,点D是OA上的一点,OC=OD=4,OA=6,点B的坐标为(4,4).动点E从点C出发,以每秒![]() 个单位长度的速度沿线段CD向点D运动,过点E作BC的垂线EF交线段BC于点F,以线段EF为斜边向右作等腰直角△EFG.设点E的运动时间为t秒(0≤t≤4).
个单位长度的速度沿线段CD向点D运动,过点E作BC的垂线EF交线段BC于点F,以线段EF为斜边向右作等腰直角△EFG.设点E的运动时间为t秒(0≤t≤4).

(1)点G的坐标为( , )(用含t的代数式表示)
(2)连接OE、BG,当t为何值时,以O、C、E为顶点的三角形与△BFG相似?
(3)设点E从点C出发时,点E、F、G都与点C重合,点E在运动过程中,当△ABG 的面积为![]() 时,求点E运动的时间t的值,并直接写出点G从出发到此时所经过的路径长 (即线段AG的长).
时,求点E运动的时间t的值,并直接写出点G从出发到此时所经过的路径长 (即线段AG的长).
【答案】(1)![]() t,4﹣
t,4﹣![]() t;(2)t=2或2
t;(2)t=2或2![]() ﹣2(3)
﹣2(3)![]()
【解析】分析:(1)依据△CDO和△CEF均为等腰直角三角形,CE=![]() t,即可得到点G的坐标;
t,即可得到点G的坐标;
(2)依据∠OCE=∠BFG=45°,分两种情况进行讨论:①若△OCE∽△BFG,则![]() ,②若△ECO∽△BFG,则
,②若△ECO∽△BFG,则![]() ,分别求得t的值即可;
,分别求得t的值即可;
(3)过点G作GH∥x轴,交AB于H,根据直线AB的解析式为y=-2x+12,根据G(![]() t,4-
t,4-![]() t),将y=4-
t),将y=4-![]() t代入y=-2x+12,可得H(4+
t代入y=-2x+12,可得H(4+![]() ,4-
,4-![]() t),再根据△ABG 的面积为
t),再根据△ABG 的面积为![]() ,即可得到t的值,进而得到点G的坐标为(
,即可得到t的值,进而得到点G的坐标为(![]() ,
,![]() ),CG=
),CG=![]() .
.
详解:(1)由题可得,△CDO和△CEF均为等腰直角三角形,
∵CE=![]() t,
t,
∴CF=EF=t,
∴点G的横坐标为CF+![]() EF=t+
EF=t+![]() t=
t=![]() t,纵坐标为CO-
t,纵坐标为CO-![]() EF=4-
EF=4-![]() t,
t,
∴G(![]() t,4-
t,4-![]() t),
t),
故答案为:![]() t,4-
t,4-![]() t;
t;
(2)∵CE=![]() t,
t,
∴EF=CF=t,FG=![]() t,BF=4-t,
t,BF=4-t,
∵∠OCE=∠BFG=45°,
①若△OCE∽△BFG,则![]() ,
,
即![]() ,解得t=2;
,解得t=2;
②若△ECO∽△BFG,则![]() ,
,
即![]() ,解得t=2
,解得t=2![]() -2;
-2;
综上所述,当t=2或2![]() -2时,以O、C、E为顶点的三角形与△BFG相似;
-2时,以O、C、E为顶点的三角形与△BFG相似;
(3)如图,过点G作GH∥x轴,交AB于H,
设直线AB的解析式为y=kx+b,则
![]() ,解得
,解得![]() ,
,
∴y=-2x+12,
∵G(![]() t,4-
t,4-![]() t),将y=4-
t),将y=4-![]() t代入y=-2x+12,可得x=4+
t代入y=-2x+12,可得x=4+![]() ,
,
∴H(4+![]() ,4-
,4-![]() t),
t),
∴GH=|4+![]() -
-![]() t|,
t|,
∴S△ABG=![]() GH×BD=
GH×BD=![]() |4+
|4+![]() -
-![]() t|×4=2|4-
t|×4=2|4-![]() t|,
t|,
又∵△ABG 的面积为![]() ,
,
∴2|4-![]() t|=
t|=![]() ,
,
解得t=![]() 或t=
或t=![]() (舍去),
(舍去),
此时,点G的坐标为(![]() ,
,![]() ),CG=
),CG=![]() .
.
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点A在x轴上,点C在y轴上,点B的坐标是![]() ,将
,将![]() 沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.
沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.

(1)求直线OB的解析式及线段OE的长.
(2)求直线BD的解析式及点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )

A. 第24天的销售量为200件 B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等 D. 第30天的日销售利润是750元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.
班级 | 平均数(分) | 中位数 | 众数 |
九(1) | 85 | 85 | |
九(2) | 80 |
(1)根据图示填写上表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班级的成绩较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
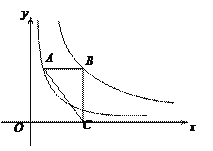
【题目】如图,点A在反比例函数y=![]() (x>0)的图像上,点B在反比例函数y=
(x>0)的图像上,点B在反比例函数y=![]() (x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
(x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
A. 10 B. 12 C. 14 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图形中每一小格正方形的边长为1,已知△ABC
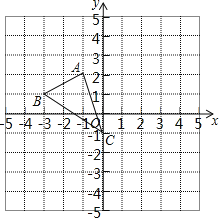
(1)AC的长等于 .(结果保留根号)
(2)将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 ;
(3)画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,并写出A点对应点A1的坐标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中, AB=8,BC=4,P,Q分别是直线AB,AD上的两个动点,点![]() 在边
在边![]() 上,
上,![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 的最小值为( )
的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com