
【题目】如图,已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,AC=4,CD=3,则AB﹣AD=_____.
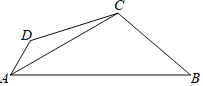
【答案】2![]() .
.
【解析】
利用“截长补短”中的补短,补出邻补角即可出现相等角度,求出△DEC≌△BFC和△EAC≌△FAC,推出DE=BF,AE=AF,求出AB﹣AD=2DE,求出DE即可.
解:过C作CE⊥AD交AD的延长线于E,CF⊥BA于F,则∠E=∠CFB=90°,
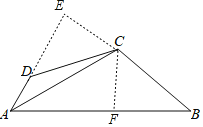
∵AC平分∠DAB,
∴CE=CF,
∵∠B与∠ADC互补,
∴∠B+∠ADC=180°,
∵∠ADC+∠EDC=180°,
∴∠B=∠EDC,
在△DEC和△BFC中
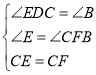
∴△DEC≌△BFC,
∴DE=BF,
∵AC平分∠DAB,
∴∠EAC=∠FAC=![]()
在△EAC和△FAC中
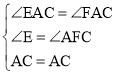
∴△EAC≌△FAC,
∴AE=AF,
∴AB﹣AD=(AF+BF)﹣(AE﹣DE)=(AE+DE)﹣(AE﹣DE)=2DE,
∵在Rt△AEC中,∠E=90°,∠EAC=30°,AC=4,
∴CE=![]() AC=2,
AC=2,
在Rt△DEC中,∠E=90°,DC=3,CE=2,
由勾股定理得:DE=![]() =
=![]() =
=![]() ,
,
∴AB﹣AD=2DE=2![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:二次函数图象的顶点坐标是(3,5),且抛物线经过点A(1,3).
(1)求此抛物线的表达式;
(2)如果点A关于该抛物线对称轴的对称点是B点,且抛物线与y轴的交点是C点,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是反比例函数y=![]() 图象上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=
图象上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=![]() OC,S四边形ABCD=9,则k值为( )
OC,S四边形ABCD=9,则k值为( )
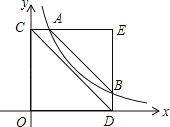
A.8B.10C.12D.16.
查看答案和解析>>
科目:初中数学 来源: 题型:
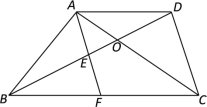
【题目】如图,在梯形ABCD中,AD//BC,AC与BD相交于点O,点E在线段OB上,AE的延长线与BC相交于点F,OD2 = OB·OE.
(1)求证:四边形AFCD是平行四边形;
(2)如果BC=BD,AE·AF=AD·BF,求证:△ABE∽△ACD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径![]() 米是其两腿迈出的步长之差
米是其两腿迈出的步长之差![]() 厘米
厘米![]() 的反比例函数,其图象如图所示.
的反比例函数,其图象如图所示.
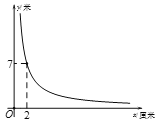
请根据图象中的信息解决下列问题:
(1)求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当某人两腿迈出的步长之差为![]() 厘米时,他蒙上眼睛走出的大圆圈的半径为______米;
厘米时,他蒙上眼睛走出的大圆圈的半径为______米;
(3)若某人蒙上眼睛走出的大圆圈的半径不小于![]() 米,则其两腿迈出的步长之差最多是多少厘米?
米,则其两腿迈出的步长之差最多是多少厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
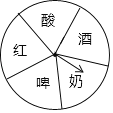
【题目】某超市为了答谢顾客发起活动:凡在本超市一次性购物满100元的顾客,当天均可凭购物小票参与一次抽奖活动,奖品是三种瓶装饮品:红酒、啤酒和酸奶,抽奖规则如下:
①如图,是一个材质均匀可自出转动的转盘,转盘被等分成五个扇形区域,各区域上分别写有“红”、“啤”、“酒”、“酸”、“奶”字样;
②参与一次奖活动的顾客可以进行两次“随机转动”,但若转盘停止时指针指向两边区域的边界则可以重新转动转盘,直到指针停到有字的区域才算完成了这次随机转动;
③顾客参与一次抽奖活动,记录两次指针所指区域对应的字,若这两个字和某种奖品名称对应的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;若两字不能组成一种奖品名时,不能获得任何奖品,根据以上规则,回答下列问题:
(1)求只做一次“随机转动”指针指向“酒“字的概率;
(2)请用列表或画树状图的方法求顾客参与一次抽奖活动获得一瓶红酒的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
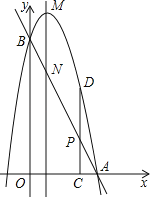
【题目】如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线y=﹣2x2+bx+c过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D,抛物线的顶点为M,其对称轴交AB于点N.
(1)求抛物线的表达式及点M、N的坐标;
(2)是否存在点P,使四边形MNPD为平行四边形?若存在求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形![]() 中,已知
中,已知![]() ,点
,点![]() 为
为![]() 边上一点,满足
边上一点,满足![]() ,动点
,动点![]() 以
以![]() 的速度沿线段
的速度沿线段![]() 从点
从点![]() 移动到点
移动到点![]() ,连接
,连接![]() ,作
,作![]() ,交线段
,交线段![]() 于点
于点![]() ,设点
,设点![]() 移动的时间为
移动的时间为![]() ,
,![]() 的长度为
的长度为![]() ,
,![]() 与
与![]() 的函数关系如图②所示.
的函数关系如图②所示.
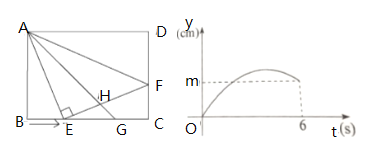
(1)图①中,![]() _______
_______![]() ,图②中,
,图②中,![]() _______;
_______;
(2)点![]() 能否为线段
能否为线段![]() 的中点?若可能,求出此时
的中点?若可能,求出此时![]() 的值,若不可能,请说明理由;
的值,若不可能,请说明理由;
(3)在图①中,连接![]() 、
、![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() 平分
平分![]() 的面积,求此时
的面积,求此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
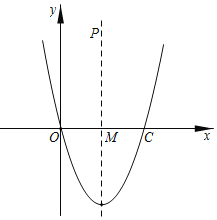
【题目】已知抛物线顶点坐标为(2,﹣4),且与x轴交于原点和点C,对称轴与x轴交点为M.
(1)求抛物线的解析式;
(2)A点在抛物线上,且A点的横坐标为﹣2,在抛物线对称轴上找一点B,使得AB与CB的差最大,求B点的坐标;
(3)P点在抛物线的对称轴上,且P点的纵坐标为8.探究:在抛物线上是否存在点Q使得O、M、P、Q四点共圆,若存在求出Q点坐标;若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com