
【题目】如图,△ABC中,∠C=90°.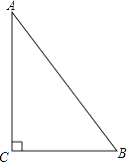
(1)在BC边上作一点P,使得点P到点C的距离与点P到边AB的距离相等(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AC=8,BC=6,求CP的长.
【答案】
(1)解:如图,点P即为所求
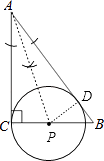
(2)解:作PD⊥AB于点,如图, 
∵AP平分∠CAB,PD⊥AB于D,∠C=90°,
∴PD=PC.
在Rt△ADP和Rt△ACP中
![]() ,
,
∴Rt△ADP≌Rt△ACP(HL),
∴AD=AC=8,
在Rt△ABC中,AB= ![]() =10,
=10,
∴BD=10﹣8=2,
设PC=x,则PD=x,BP=6﹣x,
在Rt△BDP中,∵PD2+BD2=PB2,
∴(6﹣x)2=x2+22,解得x= ![]() .
.
答:CP的长为 ![]()
【解析】(1)根据角平分线的性质作图,作∠BAC的平分线交BC于P点,则点P到点C的距离与点P到边AB的距离相等。
(2)添加辅助线,过点点P作PD⊥AB于点D,根据角平分线性质得PD=PC,则可证明Rt△ADP≌Rt△ACP得到AD=AC=8,再利用勾股定理计算出AB=10,则BD=2,设PC=x,则PD=x,BP=6-x,在Rt△BDP中,利于勾股定理得建立方程,然后解方程即可。
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
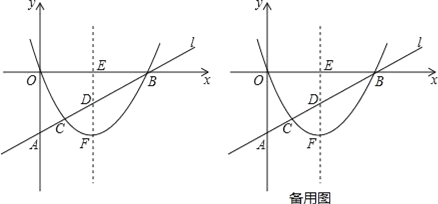
【题目】如图,已知:在平面直角坐标系中,直线l与y轴相交于点A(0,m)其中m<0,与x轴相交于点B(4,0).抛物线y=ax2+bx(a>0)的顶点为F,它与直线l相交于点C,其对称轴分别与直线l和x轴相交于点D和点E.
(1)设a=![]() ,m=﹣2时,
,m=﹣2时,
①求出点C、点D的坐标;
②抛物线y=ax2+bx上是否存在点G,使得以G、C、D、F四点为顶点的四边形为平行四边形?如果存在,求出点G的坐标;如果不存在,请说明理由.
(2)当以F、C、D为顶点的三角形与△BED相似且满足三角形FAC的面积与三角形FBC面积之比为1:3时,求抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )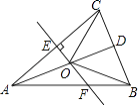
A.1对
B.2对
C.3对
D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点A(1,2).
(1)求m、n的值;
(2)设l1交x轴于点B,l2交x轴于点C,若点D与点A,B,C能构成平行四边形,请直接写出D点坐标;
(3)请在所给坐标系中画出直线l1和l2 , 并根据图象回答问题:
当x满足时,y1>2;
当x满足时,0<y2≤3;
当x满足时,y1<y2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老王以每千克0.8元的价格从批发市场购进若干千克西瓜到市场销售,在销售了部分西瓜后,余下的每千克降价0.2元,全部售完,销售金额与卖瓜的千克数之间的关系如图所示,那么老王赚了( ) 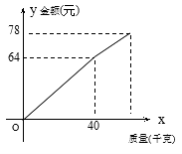
A.32元
B.36元
C.38元
D.44元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一元二次方程x2﹣4x+3=0的两个实数根分别是a、b,则一次函数y=abx+a+b的图象一定不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com