
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣6上时,线段BC扫过的面积为cm2 . 
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,平行四边形ABCD的顶点A(0,2)、B(1,0)在x轴、y轴上,另两个顶点C、D在第一象限内,且AD=3AB.若反比例函数y=kx-1(k>0)的图象经过C,D两点,则k的值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈尔滨市10月份平均气温为4℃,11月份平均气温为﹣10℃,则11月份的平均气温比10月份的平均气温低( )℃.
A.﹣14B.14C.﹣6D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD是长方形纸片的四个顶点,点E、F、H分别是边AB、BC、AD上的三点,连结EF、FH.
(1)将长方形纸片的ABCD按如图①所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B′、C′、D′,点B′在F C′上,则∠EFH的度数为 ;
(2)将长方形纸片的ABCD按如图②所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B′、C′、D′(B′、C′的位置如图所示),若∠B′FC′=18°,求∠EFH的度数;
(3)将长方形纸片的ABCD按如图③所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B′、C′、D′(B′、C′的位置如图所示),若∠EFH=β°,求∠B′FC′的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A. x2﹣4=(x+4)(x﹣4) B. x2+x+1=(x+1)2
C. x2﹣2x﹣3=(x﹣1)2﹣4 D. 2x+4=2(x+2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.
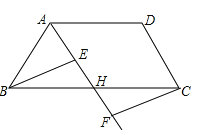
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是 ,并证明.
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com