
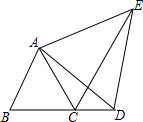
 如图,等边△ABC,点D在BC的延长线上,连接AD,以AD为边作等边△ADE,连接CE
如图,等边△ABC,点D在BC的延长线上,连接AD,以AD为边作等边△ADE,连接CE分析 (1)利用等边三角形的性质即可证得∠BAD=∠CAE,然后利用SAS即可证明△ABD≌△ACE,进一步得出结论;
(2)根据△ABD≌△ACE可以证得∠B=∠ACE=∠ACB=60°,则∠ECD的度数即可求解.
解答 解:(1)△ABD与△ACE全等,
∵△ABC和△ADE为等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,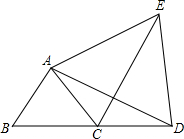
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)∵△ABD≌△ACE,
∴∠B=∠ACE=60°
又∵∠ACB=60°,
∴∠ECD=180°-60°-60°=60°,
∴∠ECD的度数不会变化.
点评 本题考查了全等三角形的判定与性质以及等边三角形的性质,正确证明∠BAD=∠CAE是证明的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
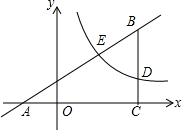 如图,在直角坐标系中,Rt△ABC的边AC在x轴上,tanA=$\frac{1}{2}$,∠ACB=90°,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象与BC边交于点D,与AB边交于点E,点D,E的横坐标分别为4,2.△BDE的面积为2.
如图,在直角坐标系中,Rt△ABC的边AC在x轴上,tanA=$\frac{1}{2}$,∠ACB=90°,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象与BC边交于点D,与AB边交于点E,点D,E的横坐标分别为4,2.△BDE的面积为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
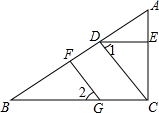 如图,如果∠1=∠2,DE∥BC,则下列结论正确的个数为( )
如图,如果∠1=∠2,DE∥BC,则下列结论正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
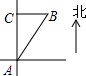 如图,一艘轮船在A处发现有一灯塔C在正北方向上,它沿北偏东30°方向以20海里/时的速度航行1小时后到达B处,发现灯塔C在正西方向上,则此时轮船与灯塔C的距离为20海里.
如图,一艘轮船在A处发现有一灯塔C在正北方向上,它沿北偏东30°方向以20海里/时的速度航行1小时后到达B处,发现灯塔C在正西方向上,则此时轮船与灯塔C的距离为20海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
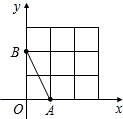 如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
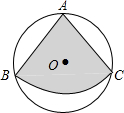 如图,从一个直径为4的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )
如图,从一个直径为4的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向空中抛2枚同样的一元硬币,如果落地后一正一反 | |
| B. | 在“石头、剪刀、布”的游戏中,小明随机出“剪刀” | |
| C. | 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是红球 | |
| D. | 掷一个质地均匀的正六面体骰子,向上的面点数是大于4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com