
 接PB,试证明:△PBE为等腰三角形;
接PB,试证明:△PBE为等腰三角形;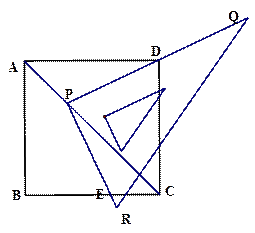
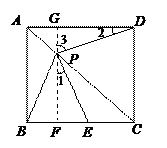
 分
分 
 =∠PAD=45° AP=AP
=∠PAD=45° AP=AP 分
分 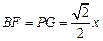 ,
,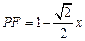 ………7分
………7分 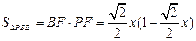
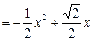 .
. 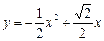 (
(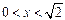 )………8分
)………8分 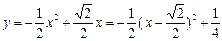 .
. 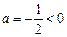 ,
,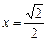 时,
时,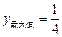 ………9分
………9分 

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源:不详 题型:解答题
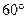 方向航行10km至B港,再沿北偏西
方向航行10km至B港,再沿北偏西 方向航行10km到达C港.
方向航行10km到达C港. (1)求A、C两港之间的距离(精确到1km)
(1)求A、C两港之间的距离(精确到1km)查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
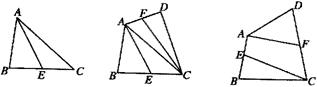
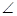 A=90
A=90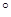 ,AB=4,AC=3,D在BC上运动(不与B、C重合),过D点分别向AB、Ac作垂线,垂足分别为E、F,则矩形AEDF的面积的最大值为___________。
,AB=4,AC=3,D在BC上运动(不与B、C重合),过D点分别向AB、Ac作垂线,垂足分别为E、F,则矩形AEDF的面积的最大值为___________。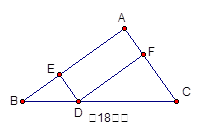
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 状并证明;
状并证明; B,求证:梯形ABCD是等腰梯形.
B,求证:梯形ABCD是等腰梯形.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 AD⊥BC,垂足为D,AE∥BC, DE∥AB.
AD⊥BC,垂足为D,AE∥BC, DE∥AB.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
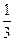 AB,
AB,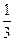 CD,连接AF,CE(如图5),则四边形AECF的面积是 ;
CD,连接AF,CE(如图5),则四边形AECF的面积是 ; ABCD的面积是2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动,点F从点B出发沿BC以每秒
ABCD的面积是2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动,点F从点B出发沿BC以每秒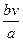 个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.
个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.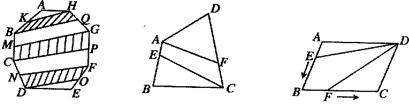
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com