解:(1)二次函数y=x
2-2x-3=(x-1)
2-4,图象的顶点坐标为(1,-4),
二次函数y=-x
2+4x-7=-(x-2)
2-3图象的顶点坐标为(2,-3),
①当x=1时,y=-x
2+4x-7=-4,
∴点(1,-4)二次函数y=-x
2+4x-7图象上,
②当x=2时,y=x
2-2x-3=-3,
∴点(2,-3)在二次函数y=x
2-2x-3图象上,
所以,二次函数y=x
2-2x-3图象与二次函数y=-x
2+4x-7图象相伴随.
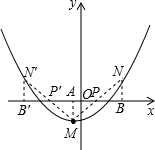
(2)①∵旋转前后的两个函数图象相伴随,
∴y
2的图象的顶点N必在二次函数y
1=

(x+1)
2-2图象上,
∵y
2的图象是二次函数y
1=

(x+1)
2-2图象绕点P旋转180°得到,
∴这两个函数图象的顶点M、N关于点P对称,
∴如图,y
2图象的顶点可能位于y
1=

(x+1)
2-2图象对称轴的右侧(点N)或左侧(点N′),
分别过M、N作MA⊥x轴,NB⊥x轴,垂足分别为A、B,
∵在△APM和△BPN中,
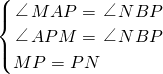
,
∴△APM≌△BPN(AAS),
∴NB=AM=2,
同理可求,N′B′=AM=2,
当y=2时,

(x+1)
2-2=2,
解得 x
1=3,x
2=-5,
∴N(3,2),N′(-5,2),
当N是y
2图象顶点时,
设y
2=a(x-3)
2+2(a≠0),
把M(-1,-2)代入关系式,得:
a=-

,
∴y
2=-

(x-3)
2+2,
当N′是y
2图象顶点时,同理可求,y
2=-

(x+5)
2+2,
综上所述,y
2=-

(x-3)
2+2或y
2=-

(x+5)
2+2,
②设点Q的坐标为(0,m),则MN
2=32,MQ
2=m
2+4m+5,
i:当点N取(3,2)时,NQ
2=m
2-4m+13,
令MQ
2=NQ
2,则m
2+4m+5=m
2-4m+13,m=1,
∴MQ
2+NQ
2=20≠MN
2,
∴当N(3,2)时,不存在符合条件的Q点,使得△MNQ是等腰直角三角形;
ii:当点N取(-5,2)时,NQ
2=m
2-4m+29,
令MQ
2=NQ
2,则m
2+4m+5=m
2-4m+29,m=3,
∴MQ
2+NQ
2=52≠MN
2,
∴当N(-5,2)时,不存在符合条件的Q点,使得△MNQ是等腰直角三角形;
综上所述,不存在符合条件的Q点,使得△MNQ是等腰直角三角形.
分析:(1)根据图象相伴随的定义分析结合两函数的解析式求出顶点坐标,进而分析得出即可;
(2)①根据旋转的性质得出这两个函数图象的顶点M、N关于点P对称,即可得出N点、N′点坐标,再利用图象过M点进而得出解析式;
②设点Q的坐标为(0,m),则MN
2=32,MQ
2=m
2+4m+5,利用当点N取(3,2)时,以及当点N取(-5,2)时,分别求出即可.
点评:此题主要考查了二次函数的综合应用以及勾股定理和全等三角形的判定与性质以及等腰直角三角形的性质等知识,利用数形结合和分类讨论的思想得出是解题关键.

 (x+1)2-2图象的顶点为M,点P是x轴上一个动点,将二次函数y1的图象绕点P旋转180°得到一个新的二次函数y2的图象,且旋转前后的两个函数图象相伴随,y2的图象的顶点为N.
(x+1)2-2图象的顶点为M,点P是x轴上一个动点,将二次函数y1的图象绕点P旋转180°得到一个新的二次函数y2的图象,且旋转前后的两个函数图象相伴随,y2的图象的顶点为N.
 (x+1)2-2图象上,
(x+1)2-2图象上, (x+1)2-2图象绕点P旋转180°得到,
(x+1)2-2图象绕点P旋转180°得到, (x+1)2-2图象对称轴的右侧(点N)或左侧(点N′),
(x+1)2-2图象对称轴的右侧(点N)或左侧(点N′),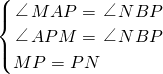 ,
, (x+1)2-2=2,
(x+1)2-2=2, ,
, (x-3)2+2,
(x-3)2+2, (x+5)2+2,
(x+5)2+2, (x-3)2+2或y2=-
(x-3)2+2或y2=- (x+5)2+2,
(x+5)2+2,