
 如图,△AGB中,以边AG、AB为边分别作正方形AEFG、正方形ABCD,线段EB和GD相交于点H,tan∠AGB=
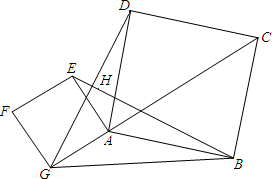
如图,△AGB中,以边AG、AB为边分别作正方形AEFG、正方形ABCD,线段EB和GD相交于点H,tan∠AGB= ,点G、A、C在同一条直线上.
,点G、A、C在同一条直线上. ,求BE的长.
,求BE的长.


 ,
, ,
,
 ,OG=4
,OG=4 ,
, ,BD=6
,BD=6 ,
, .
. 设BO=3x,则GO=4x根据GA=4x-3x=
设BO=3x,则GO=4x根据GA=4x-3x= ,求出x=
,求出x= 求出GD=5
求出GD=5 ,BD=6
,BD=6 ,根据△GAD≌△EAB得出BE=GD,代入求出即可.
,根据△GAD≌△EAB得出BE=GD,代入求出即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 (2012•龙湾区二模)如图,在Rt△AGB中,∠G=90°,∠A=30°,以GB为边在GB的下方作正方形GBEH,HE交AB于点F,以AB为边在AB的上方作正方形ABCD,连接CG,若GB=1,则CG2=
(2012•龙湾区二模)如图,在Rt△AGB中,∠G=90°,∠A=30°,以GB为边在GB的下方作正方形GBEH,HE交AB于点F,以AB为边在AB的上方作正方形ABCD,连接CG,若GB=1,则CG2=| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:[名校联盟]2013届重庆市重庆一中九年级下学期定时作业数学试卷(带解析) 题型:解答题
如图,△AGB中,以边AG、AB为边分别作正方形AEFG、正方形ABCD,线段EB和GD相交于点H, tan∠AGB= ,点G、A、C在同一条直线上.
,点G、A、C在同一条直线上.
(1)求证:EB⊥GD;
(2)若∠AG=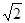 ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年重庆市九年级下学期定时作业数学试卷(解析版) 题型:解答题
如图,△AGB中,以边AG、AB为边分别作正方形AEFG、正方形ABCD,线段EB和GD相交于点H, tan∠AGB=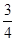 ,点G、A、C在同一条直线上.
,点G、A、C在同一条直线上.

(1)求证:EB⊥GD;
(2)若∠AG=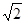 ,求BE的长.
,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com