
分析 (1)首先设购买一件甲商品需x元,购买一件乙商品需要y元,由题意得等量关系:①2件甲商品的费用+3件乙商品的费用=340;②4件甲商品的费用+5件乙商品的费用=600,根据等量关系列出方程组,再解即可;
(2)首先设该商场可以购买a件乙商品,则可以购买甲种商品(100-a)件,由题意得不等关系:甲商品的总费用+乙商品的总费用≤7000,再列出不等式,求解即可.
解答 解:(1)设购买一件甲商品需x元,购买一件乙商品需要y元,
根据题意,得:$\left\{\begin{array}{l}{2x+3y=340}\\{4x+5y=600}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=50}\\{y=80}\end{array}\right.$,
答:购买一件甲商品需50元,购买一件乙商品需要80元.
(2)设该商场可以购买a件乙商品,则可以购买甲种商品(100-a)件,
根据题意,得:50(100-a)+80a≤7000
解得:a≤66$\frac{2}{3}$,
答:该商场最多可以购买66件乙商品.
点评 此题主要考查了二元一次方程组和一元一次不等式的应用,关键是正确理解题意,找出题目中的等量关系和不等关系,列出方程组和不等式.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
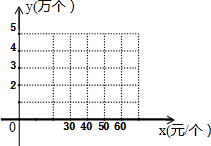 某公司销售一种进价为20(元/个)的计算器,其销售量y(万个)与销售价格x(元/个)的变化如表:
某公司销售一种进价为20(元/个)的计算器,其销售量y(万个)与销售价格x(元/个)的变化如表:| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两条边分别相等的两个等腰三角形全等 | |
| B. | 两腰对应相等的两个等腰三角形全等 | |
| C. | 有两条边分别相等的两个直角三角形全等 | |
| D. | 斜边和一条直角边对应相等的两个直角三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
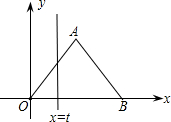 如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )
如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )| A. | 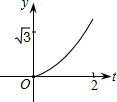 | B. | 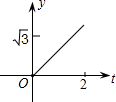 | C. | 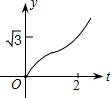 | D. | 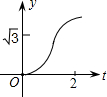 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,添加条件不能判断△ACD≌△ABE的是( )
如图,添加条件不能判断△ACD≌△ABE的是( )| A. | ∠AEB=∠ADC,CD=BE | B. | AC=AB,AD=AE | C. | AC=AB,∠C=∠B | D. | ∠AEB=∠ADC,∠C=∠B |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com