
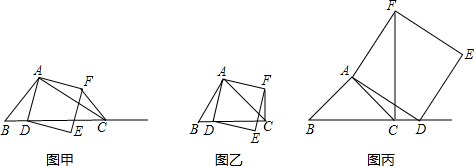
分析 (1)①由四边形ADEF是正方形与AB=AC,∠BAC=90°,易证得△BAD≌△CAF,然后由全等三角形的性质,可证得CF=BD,继而求得∠BCA+∠ACF=90°,即CF⊥BD;
②由四边形ADEF是正方形与AB=AC,∠BAC=90°,易证得△BAD≌△CAF,然后由全等三角形的性质,可证得CF=BD,继而求得∠BCA+∠ACF=90°,即CF⊥BD.
(2)当∠ACB=45°时,过点A作AG⊥AC交CB或CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①可知CF⊥BD.
(3)如图4,作辅助线,构建等腰直角三角形,说明△ABC是钝角三角形,求AQ、BQ、AB的长,用面积法求出AB上的高为$\frac{12\sqrt{17}}{17}$.
解答 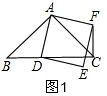 解:(1)如图1,∵四边形ADEF是正方形,
解:(1)如图1,∵四边形ADEF是正方形,
∴∠DAF=90°,AD=AF,
∵AB=AC,∠BAC=90°,
∴∠BAD+∠DAC=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△BAD≌△CAF(SAS),
∴CF=BD,
∴∠B=∠ACF,
∴∠B+∠BCA=90°,
∴∠BCA+∠ACF=90°,
即CF⊥BD;
故答案为:垂直,相等;
②当点D在BC的延长线上时,①的结论仍成立.
如图2,由正方形ADEF得:AD=AF,∠DAF=90°.
∵∠BAC=90°,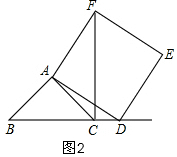
∴∠DAF=∠BAC.
∴∠DAB=∠FAC.
又∵AB=AC,
∴△DAB≌△FAC(SAS).
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACF=45°.
∴∠BCF=∠ACB+∠ACF=90°,
即 CF⊥BD.
(2)当∠BCA=45°时,CF⊥BD;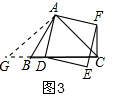
理由如下:
如图3,过点A作AC的垂线与CB所在直线交于G,
∵∠ACB=45°,
∴△AGC等腰直角三角形,
∴AG=AC,∠AGC=∠ACG=45°,
∵AG=AC,AD=AF,
∵∠GAD=∠GAC-∠DAC=90°-∠DAC,∠FAC=∠FAD-∠DAC=90°-∠DAC,
∴∠GAD=∠FAC,
∴△GAD≌△CAF(SAS),
∴∠ACF=∠AGD=45°,
∴∠GCF=∠GCA+∠ACF=90°,
∴CF⊥BC;
(3)当具备∠BCA=45°,AC=4$\sqrt{2}$,BC=3时,
如图4,过点A作AQ⊥BC交CB的延长线于点Q,
∵∠BCA=45°,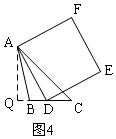
∴AQ=CQ=4.
∴△ABC为钝角三角形,
∴BQ=1,
由勾股定理得:则AB=$\sqrt{A{Q}^{2}+B{Q}^{2}}$=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,
设AB边上的高为h,
S△ABC=$\frac{1}{2}$AB•h=$\frac{1}{2}$BC•AQ,
∴$\frac{1}{2}$×$\sqrt{17}$h=$\frac{1}{2}$×3×4,
∴h=$\frac{12\sqrt{17}}{17}$,
答:△ABC中AB边上的高为$\frac{12\sqrt{17}}{17}$.
点评 本题考查了全等三角形的判定和性质,正方形的性质,余角的性质,勾股定理,等腰直角三角形的性质和判定,第2问过点A作AG⊥AC交CB的延长线于点G构造全等三角形是解题的关键;运用了类比的方法,利用三角形全等解决问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
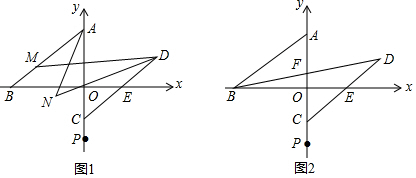
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
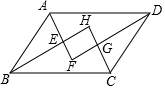 如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.在不添加其他条件的情况下,试写出上述条件推出的结论,并选择你喜欢的一个结论说明成立的理由.(要求推理过程中用到″平行四边形″和″角平分线″这两个条件).
如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.在不添加其他条件的情况下,试写出上述条件推出的结论,并选择你喜欢的一个结论说明成立的理由.(要求推理过程中用到″平行四边形″和″角平分线″这两个条件).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
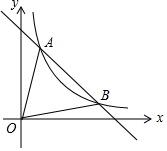 如图,由正比例函数y=-x沿y轴的正方向平移4个单位而成的一次函数y=-x+b的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.
如图,由正比例函数y=-x沿y轴的正方向平移4个单位而成的一次函数y=-x+b的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com