
计算用一种正多边形拼成平整、无隙的图案,你能设计出几种方案?画出草图.
见解析
【解析】本题考查了平面镶嵌的条件
分别求出各个正多边形的每个内角的度数,结合镶嵌的条件即可作出判断.
A、正三角形的每个内角是60°,能整除360°,6个能密铺;
B、正方形的每个内角是90°,能整除360°,4个能密铺;
C、正五边形每个内角是180°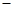 360°÷5=108°,不能整除360°,不能密铺;
360°÷5=108°,不能整除360°,不能密铺;
D、正六边形每个内角为120度,能整除360度,3个能密铺.
B、正七边形每个内角是:180°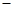 360°÷7=
360°÷7=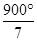 ,不能整除360°,不能密铺;
,不能整除360°,不能密铺;
C、正八边形每个内角是:180°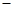 360°÷8=135°,不能整除360°,不能密铺;
360°÷8=135°,不能整除360°,不能密铺;
D、正九边形每个内角是:180° 360°÷9=140°,不能整除360°,不能密铺;
360°÷9=140°,不能整除360°,不能密铺;
故三种方案:用三个正六边形或四个正四边形或六个正三角形可拼成平整、无隙的图案,图案略。


 计算高手系列答案
计算高手系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com