

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:单选题
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
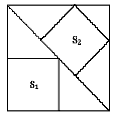
| A.S1> S2 | B. S1 = S2 |
| C. S1< S2 | D. S1、S2的大小关系不确定 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

 、①②都错
、①②都错查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 填空:
填空:
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与AD重合,由旋转可得:
与AD重合,由旋转可得: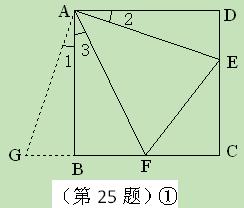
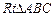 沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=
沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=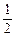 ∠DAB.试猜想DE,BF,EF之间有何数量
∠DAB.试猜想DE,BF,EF之间有何数量 关系,并证明你的猜想.
关系,并证明你的猜想.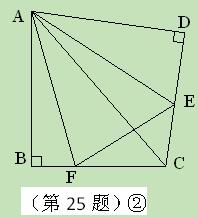
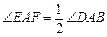 ,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).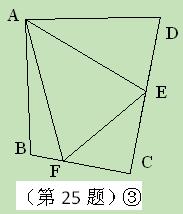
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com