
”¾ĢāÄæ”æijÖÖŠĶŗŵÄĪĀæŲĖ®ĻäµÄ¹¤×÷¹ż³ĢŹĒ£ŗ½ÓĶصēŌ“ŗó£¬ŌŚ³õŹ¼ĪĀ¶Č20”ęĻĀ¼ÓČČĖ®ĻäÖŠµÄĖ®£»µ±Ė®ĪĀ“ļµ½Éč¶ØĪĀ¶Č80”ꏱ£¬¼ÓČČĶ£Ö¹£»“ĖŗóĖ®ĻäÖŠµÄĖ®ĪĀæŖŹ¼Öš½„ĻĀ½µ£¬µ±ĻĀ½µµ½20”ꏱ£¬ŌŁ“Ī×Ō¶Æ¼ÓČČĖ®ĻäÖŠµÄĖ®ÖĮ80”ꏱ£¬¼ÓČČĶ£Ö¹£»µ±Ė®ĻäÖŠµÄĖ®ĪĀĻĀ½µµ½20”ꏱ£¬ŌŁ“Ī×Ō¶Æ¼ÓČČ£¬”£¬°“ÕÕŅŌÉĻ·½Ź½²»¶ĻŃ»·£®
Š”Ć÷øł¾ŻŃ§Ļ°ŗÆŹżµÄ¾Ń飬¶ŌøĆŠĶŗÅĪĀæŲĖ®ĻäÖŠµÄĖ®ĪĀĖꏱ¼ä±ä»ÆµÄ¹ęĀɽųŠŠĮĖĢ½¾æ£®·¢ĻÖĖ®ĪĀyŹĒŹ±¼äxµÄŗÆŹż£¬ĘäÖŠy£Øµ„Ī»£ŗ”ę£©±ķŹ¾Ė®ĻäÖŠĖ®µÄĪĀ¶Č£®x£Øµ„Ī»£ŗmin£©±ķŹ¾½ÓĶصēŌ“ŗóµÄŹ±¼ä£®
ĻĀĆęŹĒŠ”Ć÷µÄĢ½¾æ¹ż³Ģ£¬Ēė²¹³äĶźÕū£ŗ
£Ø1£©ĻĀ±ķ¼ĒĀ¼ĮĖ32minÄŚ14øöŹ±¼äµćµÄĪĀæŲĖ®ĻäÖŠĖ®µÄĪĀ¶ČyĖꏱ¼äxµÄ±ä»ÆĒéæö
½ÓĶصēŌ“ŗóµÄŹ±¼äx£Øµ„Ī»£ŗmin£© | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | ” |
Ė®ĻäÖŠĖ®µÄĪĀ¶Čy£Øµ„Ī»£ŗ”ę£© | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | ” |
mµÄÖµĪŖ £»
£Ø2£©¢Łµ±0”Üx”Ü4Ź±£¬Š“³öŅ»øö·ūŗĻ±ķÖŠŹż¾ŻµÄŗÆŹż½āĪöŹ½ £»
µ±4£¼x”Ü16Ź±£¬Š“³öŅ»øö·ūŗĻ±ķÖŠŹż¾ŻµÄŗÆŹż½āĪöŹ½ £»
¢ŚČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ćč³öĮĖÉĻ±ķÖŠ²æ·ÖŹż¾Ż¶ŌÓ¦µÄµć£¬øł¾ŻĆč³öµÄµć£¬»³öµ±0”Üx”Ü32Ź±£¬ĪĀ¶ČyĖꏱ¼äx±ä»ÆµÄŗÆŹżĶ¼Ļó£ŗ
£Ø3£©Čē¹ūĖ®ĪĀyĖꏱ¼äxµÄ±ä»Æ¹ęĀɲ»±ä£¬Ō¤²āĖ®ĪĀµŚ8“Ī“ļµ½40”ꏱ£¬¾ąĄė½ÓĶصēŌ“ min£®

”¾“š°ø”æ£Ø1£©50£»£Ø2£©¢Ły=15x+20£¬y=![]() £»¢ŚĶ¼Ļó¼ū½āĪö£»£Ø3£©56.
£»¢ŚĶ¼Ļó¼ū½āĪö£»£Ø3£©56.
”¾½āĪö”æ
£Ø1£©¹Ū²ģ±ķøń£¬æɵĆĆæ·ÖÖÓÉĻÉż¶ąÉŁĪĀ¶Č£¬ÓÉ“Ė¼“æɽā¾öĪŹĢā£®
£Ø2£©¢Ł¹ŲĻµ±ķøń£¬æÉÖŖŗÆŹżŹĒŅ»“ĪŗÆŹż£¬ÓÉ“ĖĄūÓĆ“ż¶ØĻµŹż·Ø½ā¾öĪŹĢā£®
¢Ś¹ŲĻµ±ķøńæÉÖŖ£¬ŗÆŹż·“±ČĄżŗÆŹż£¬ĄūÓĆ“ż¶ØĻµŹż·Ø¼“æɽā¾öĪŹĢā£®
£Ø3£©øł¾Ż±ķøń£¬ĄūÓĆĆčµć·Ø»³öĶ¼Ļó¼“æɽā¾öĪŹĢā£®
£Ø4£©ĄūÓĆĶ¼ĻóŃ°ÕŅ¹ęĀɼ“æɽā¾ö£®
£Ø1£©ÓÉĢāŅāæÉÖŖ2·ÖÖÓĪĀ¶ČÉĻÉż30”ę£¬ĖłŅŌm=50£¬
¹Ź“š°øĪŖ50£®
£Ø2£©¢Łµ±0”Üx”Ü4Ź±£¬ŗÆŹż½āĪöŹ½ŹĒŅ»“ĪŗÆŹż£¬y=15x+20£®
¢Śµ±4£¼x”Ü16Ź±£¬ŗÆŹż½āĪöŹ½ŹĒ·“±ČĄżŗÆŹży=![]() £®
£®
¹Ź“š°øĪŖy=15x+20£¬y=![]() £®
£®
£Ø3£©ŗÆŹżĶ¼ĻóČēĶ¼ĖłŹ¾£¬
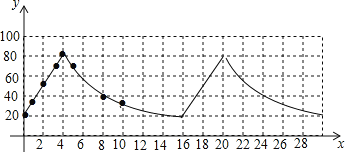
£Ø4£©¹Ū²ģĶ¼ĻóæÉÖŖŌ¤²āĖ®ĪĀµŚ8“Ī“ļµ½40”ꏱ£¬¾ąĄė½ÓĶصēŌ“56min£®
¹Ź“š°øĪŖ56£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¶ž“ĪŗÆŹży£½ax2+bx+cµÄĶ¼ĻóÓėyÖįÕż°ėÖįĻą½»£¬Ę䶄µć×ų±źĪŖ£Ø![]() £¬1£©£¬ĻĀĮŠ½įĀŪ£ŗĘäÖŠÕżČ·µÄøöŹżŹĒ£Ø””””£©
£¬1£©£¬ĻĀĮŠ½įĀŪ£ŗĘäÖŠÕżČ·µÄøöŹżŹĒ£Ø””””£©
¢Ła£¼0£»
¢Śb£¼0£»
¢Ūc£¼0£»
¢Ü![]() £»
£»
¢Ża+b+c£¼0£®
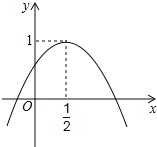
A.1 øöB.2 øöC.3 øöD.4 øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßy£½![]() x2£
x2£![]() x£3ÓėxÖįµÄ½»µćĪŖA”¢D(AŌŚDµÄÓŅ²ą)£¬ÓėyÖįµÄ½»µćĪŖC.
x£3ÓėxÖįµÄ½»µćĪŖA”¢D(AŌŚDµÄÓŅ²ą)£¬ÓėyÖįµÄ½»µćĪŖC.

(1)Ö±½ÓŠ“³öA”¢D”¢CČżµćµÄ×ų±ź£»
(2)ČōµćMŌŚÅ×ĪļĻßÉĻ£¬Ź¹µĆ”÷MADµÄĆ껿Óė”÷CADµÄĆ껿ĻąµČ£¬ĒóµćMµÄ×ų±ź£»
(3)ÉčµćC¹ŲÓŚÅ×ĪļĻ߶Ō³ĘÖįµÄ¶Ō³ĘµćĪŖB£¬ŌŚÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹µĆŅŌA”¢B”¢C”¢PĖĵćĪŖ¶„µćµÄĖıߊĪĪŖĢŻŠĪ£æČō“ęŌŚ£¬ĒėĒó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB£½AC£½10cm£¬BD”ĶACÓŚµćD£¬BD£½8cm£®µćM“ÓµćA³ö·¢£¬ŃŲACµÄ·½ĻņŌČĖŁŌĖ¶Æ£¬Ķ¬Ź±Ö±ĻßPQÓɵćB³ö·¢£¬ŃŲBAµÄ·½ĻņŌČĖŁŌĖ¶Æ£¬ŌĖ¶Æ¹ż³ĢÖŠŹ¼ÖÕ±£³ÖPQ”ĪAC£¬Ö±ĻßPQ½»ABÓŚµćP”¢½»BCÓŚµćQ”¢½»BDÓŚµćF£®Į¬½ÓPM£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£Ø0£¼t”Ü5£©£®Ļ߶ĪCMµÄ³¤¶Č¼Ē×÷y¼×£¬Ļ߶ĪBPµÄ³¤¶Č¼Ē×÷yŅŅ£¬y¼×ŗĶyŅŅ¹ŲÓŚŹ±¼ätµÄŗÆŹż±ä»ÆĒéæöČēĶ¼ĖłŹ¾£®
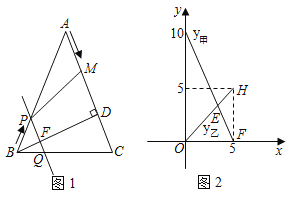
£Ø1£©ÓÉĶ¼2æÉÖŖ£¬µćMµÄŌĖ¶ÆĖŁ¶ČŹĒĆæĆė”” cm£»µ±t£½”” ĆėŹ±£¬ĖıߊĪPQCMŹĒĘ½ŠŠĖıߊĪ£æŌŚĶ¼2ÖŠ·“Ó³ÕāŅ»ĒéæöµÄµćŹĒ”” £Ø²¢Š“³ö“ĖµćµÄ×ų±ź£©£»
£Ø2£©ÉčĖıߊĪPQCMµÄĆ껿ĪŖycm2£¬ĒóyÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©Į¬½ÓPC£¬ŹĒ·ń“ęŌŚÄ³Ņ»Ź±æĢt£¬Ź¹µćMŌŚĻ߶ĪPCµÄ“¹Ö±Ę½·ÖĻßÉĻ£æČō“ęŌŚ£¬Ēó³ö“ĖŹ±tµÄÖµ£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŌŚRt”÷OABÖŠ,”ĻOAB=90”ć,”ĻBOA=30”ć,AB=2.ČōŅŌOĪŖ×ų±źŌµć,OAĖłŌŚÖ±ĻßĪŖxÖį£¬½ØĮ¢ČēĶ¼ĖłŹ¾µÄĘ½ĆęÖ±½Ē×ų±źĻµ,µćBŌŚµŚŅ»ĻóĻŽÄŚ£¬½«Rt”÷OABŃŲOBÕŪµžŗó,µćAĀäŌŚµŚŅ»ĻóĻŽÄŚµÄµćC“¦£®
£Ø1£©ĒóµćCµÄ×ų±ź£»
£Ø2£©ČōÅ×ĪļĻßy=ax2+bx£Øa”Ł0£©¾¹żC”¢AĮ½µć£¬Ēó“ĖÅ×ĪļĻߵĽāĪöŹ½£»
£Ø3£©ČōÅ×ĪļĻߵĶŌ³ĘÖįÓėOB½»ÓŚµćD£¬µćPĪŖĻ߶ĪDBÉĻŅ»µć£¬¹żP×÷yÖįµÄĘ½ŠŠĻߣ¬½»Å×ĪļĻßÓŚµćM£®ĪŹ£ŗŹĒ·ń“ęŌŚÕāŃłµÄµćP£¬Ź¹µĆĖıߊĪCDPMĪŖµČŃüĢŻŠĪ£¬Čō“ęŌŚ£¬ĒėĒó³ö“ĖŹ±µćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
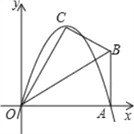
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬ŅŃÖŖµćM0µÄ×ų±źĪŖ£Ø1£¬0£©£¬½«Ļ߶ĪOM0ČĘŌµćOÄꏱÕė·½ĻņŠż×Ŗ45”ć£¬ŌŁ½«ĘäŃÓ³¤µ½M1£¬Ź¹µĆM1M0”ĶOM0£¬µĆµ½Ļ߶ĪOM1£»ÓÖ½«Ļ߶ĪOM1ČĘŌµćOÄꏱÕė·½ĻņŠż×Ŗ45”ć£¬ŌŁ½«ĘäŃÓ³¤µ½M2£¬Ź¹µĆM2M1”ĶOM1£¬µĆµ½Ļ߶ĪOM2£»Čē“ĖĻĀČ„£¬µĆµ½Ļ߶ĪOM3£¬OM4£¬OM5£¬”øł¾ŻŅŌÉĻ¹ęĀÉ£¬ĒėÖ±½ÓŠ“³öOM2014µÄ³¤¶ČĪŖ_______£®
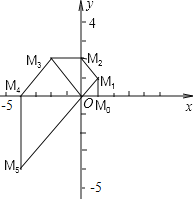
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗµćA£¬B£¬C¶¼ŌŚ”ŃOÉĻ£¬Į¬½ÓAB£¬AC£¬µćD£¬E·Ö±šŌŚAC£¬ABÉĻ£¬Į¬½ÓCE²¢ŃÓ³¤½»”ŃOÓŚµćF£¬Į¬½ÓBD£¬BF£¬”ĻBDC©”ĻBFC£½2”ĻABF£®
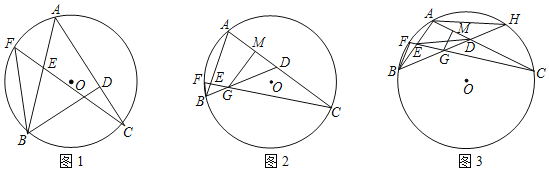
£Ø1£©ČēĶ¼1£¬ĒóÖ¤£ŗ”ĻABD£½2”ĻACF£»
£Ø2£©ČēĶ¼2£¬CE½»BDÓŚµćG£¬¹żµćG×÷GM”ĶACÓŚµćM£¬ČōAM£½MD£¬ĒóÖ¤£ŗAE£½GD£»
£Ø3£©ČēĶ¼3£¬ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬µ±AE£ŗBE£½8£ŗ7Ź±£¬Į¬½ÓDE£¬ĒŅ”ĻADE£½30”ć£®ŃÓ³¤BD½»”ŃOÓŚµćH£¬Į¬½ÓAH£¬AH£½8![]() £¬Ēó”ŃOµÄ°ė¾¶£®
£¬Ēó”ŃOµÄ°ė¾¶£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() £®µć
£®µć![]() ŌŚ
ŌŚ![]() ÉĻŅŌĆæĆė
ÉĻŅŌĆæĆė![]() øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÖÕµć
øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÖÕµć![]() ŌĖ¶Æ£®µć
ŌĖ¶Æ£®µć![]() ŃŲ
ŃŲ![]() ·½ĻņŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶Æ£¬µ±µć
·½ĻņŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶Æ£¬µ±µć![]() ²»Óėµć
²»Óėµć![]() ÖŲŗĻŹ±£¬Į¬½į
ÖŲŗĻŹ±£¬Į¬½į![]() £¬ŅŌ
£¬ŅŌ![]() £¬
£¬![]() ĪŖĮŚ±ß×÷
ĪŖĮŚ±ß×÷![]() £®µ±µć
£®µ±µć![]() Ķ£Ö¹ŌĖ¶ÆŹ±£¬µć
Ķ£Ö¹ŌĖ¶ÆŹ±£¬µć![]() Ņ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬Éčµć
Ņ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬Éčµć![]() µÄŌĖ¶ÆŹ±¼äĪŖ
µÄŌĖ¶ÆŹ±¼äĪŖ![]() £¬
£¬![]() Óė
Óė![]() ÖŲµž²æ·ÖµÄĶ¼ŠĪĆ껿ĪŖ
ÖŲµž²æ·ÖµÄĶ¼ŠĪĆ껿ĪŖ![]() £®
£®
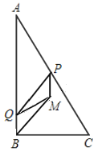
£Ø1£©µć![]() µ½±ß
µ½±ß![]() µÄ¾ąĄė
µÄ¾ąĄė![]() ””””””””£¬µć
””””””””£¬µć![]() µ½±ß
µ½±ß![]() µÄ¾ąĄė
µÄ¾ąĄė![]() ””””””””£»(ÓĆŗ¬
””””””””£»(ÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾)
µÄ“śŹżŹ½±ķŹ¾)
£Ø2£©µ±µć![]() ĀäŌŚĻ߶Ī
ĀäŌŚĻ߶Ī![]() ÉĻŹ±£¬Ēó
ÉĻŹ±£¬Ēó![]() µÄÖµ£»
掙术
£Ø3£©Ēó![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø4£©Į¬½į![]() £¬µ±
£¬µ±![]() Óė
Óė![]() µÄŅ»±ßĘ½ŠŠ»ņ“¹Ö±Ź±£¬Ö±½ÓŠ“³ö
µÄŅ»±ßĘ½ŠŠ»ņ“¹Ö±Ź±£¬Ö±½ÓŠ“³ö![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŖÉč¼ĘŅ»·łæķ20ĄåĆ×£¬³¤30ĄåĆ×µÄĶ¼°ø£¬ĘäÖŠÓŠĮ½ŗįĮ½ŹśµÄ²ŹĢõ£¬ŗį”¢Źś²ŹĢõµÄæķ¶Č±ČĪŖ2”Ć1£¬Čē¹ūŅŖŹ¹²ŹĢõĖłÕ¼Ć껿ŹĒĶ¼°øĆ껿µÄŅ»°ė£¬ÄĒĆ“Źś²ŹĢõæķ¶ČŹĒ¶ąÉŁ£æČōÉ菜²ŹĢõæķ¶ČŹĒxĄåĆ×£¬Ōņøł¾ŻĢāŅāæÉĮŠ·½³Ģ_____________£®
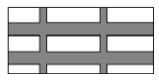
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com