
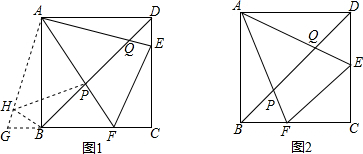
���� ��1��������ת�����ʵõ���GAB=��DAE��������֪�����õ���AEF�ա�AGF����ȫ�������ε����ʵõ�GF=EF�������������ɵõ����ۣ�
��2������ת�����ʵõ�BH=DQ����ABH=��ADB=45�㣬���ݹ��ɶ����õ�BH2+BP2=HP2����ȫ�������ε����ʵõ�PQ=HP�������������ɵõ����ۣ�
��3���ɣ�1��֪��EF=DE+BF=x+y�����ݹ��ɶ����з��̵õ���������ݣ�2���Ľ����з��̼��ɵõ����ۣ�����AC����ƽ���ߵ����ʵõ�AC��EF�������߶εĴ�ֱƽ���ߵ����ʵõ�AF=AE���Ƴ���ABP�ס�ACF�������������ε����ʵõ�$\frac{AP}{AF}=\frac{AB}{AC}$=$\frac{\sqrt{2}}{2}$��ͨ����APQ�ס�AFE�����ɵõ����ۣ�
��� ��1��֤�����ߡ�ABG�ա�ADE��
���GAB=��DAE��
�֡ߡ�BAD=90�㣬
���BAF+��DAE=90��-��EAF=90��-45��=45�㣬
���GAF=��GAB+��BAF=��EAF=45�㣬
�ڡ�GAF�͡�EAF�У�
$\left\{\begin{array}{l}{AE=AG}\\{��GAF=��EAF}\\{AF=AF}\end{array}\right.$��
���AEF�ա�AGF��
��GF=EF��
�֡�BG=DE��
��BF+DE=EF��
�ʴ�Ϊ��BF+DE=EF��
��2��BP2+DQ2=PQ2��
֤�����ߡ�ABH�ա�ADQ��
��BH=DQ����ABH=��ADB=45�㣬
�֡ߡ�ABD=45�㣬
���HBP=90�㣮
��BH2+BP2=HP2��
�ڡ�AHP�͡�AQP�У�
$\left\{\begin{array}{l}{AQ=AH}\\{��HAP=��QAP}\\{AP=AP}\end{array}\right.$��
���AHP�ա�AQP��
��PQ=HP��
��BP2+DQ2=PQ2��
�ʴ�Ϊ��BP2+DQ2=PQ2��
��3���⣺�ɣ�1��֪��EF=DE+BF=x+y��
��CE=1-x��CF=1-y����EF2=CE2+CF2��
�ࣨx+y��2=��1-x��2+��1-y��2��
��y=$\frac{1-x}{1+x}$��
��BC=CD=1��
��BD=$\sqrt{2}$��
��PB=m��DQ=n��
��PQ=$\sqrt{2}$-m-n��
�ɣ�2��֪��BP2+DQ2=PQ2��
��m2+n2=��$\sqrt{2}$-m-n��2��
��m=$\frac{2{n}^{2}-1}{{n}^{2}-2}$��n=$\frac{2{m}^{2}-1}{{m}^{2}-2}$��
����AC��
��AC��BD����EF��BD��
��AC��EF��
�ߡ�ACF=��ECA=45�㣬
���CEF=��CFE=45�㣬
��ACƽ��EF��
��AF=AE��
���FAC=��EAC���ߡ�EAF=45�㣬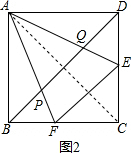
���EAC=��FAC=��BAE=22.5�㣬
�ߡ�ABD=��ACF=45�㣬
���ABP�ס�ACF��
��$\frac{AP}{AF}=\frac{AB}{AC}$=$\frac{\sqrt{2}}{2}$��
��PQ��EF��
���APQ�ס�AFE��
��$\frac{PQ}{EF}=\frac{AP}{AF}=\frac{\sqrt{2}}{2}$��
�ʴ�Ϊ��$\frac{1-x}{1+x}$��$\frac{2{n}^{2}-1}{{n}^{2}-2}$��$\frac{2{m}^{2}-1}{{m}^{2}-2}$��$\frac{\sqrt{2}}{2}$��
���� ���⿼�������������ε��ж������ʣ�ȫ�������ε��ж������ʣ������ε����ʣ����ɶ�������ת�����ʣ���������ȫ�������ε��ж��������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
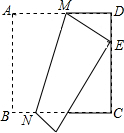 ��ͼ�����߳�Ϊ12cm��������ֽƬABCD�۵���ʹ�õ�A���ڱ�CD�ϵ�E�㣬�ۺ�ΪMN����MN�ij�Ϊ13cm����CE�ij�Ϊ7cm��
��ͼ�����߳�Ϊ12cm��������ֽƬABCD�۵���ʹ�õ�A���ڱ�CD�ϵ�E�㣬�ۺ�ΪMN����MN�ij�Ϊ13cm����CE�ij�Ϊ7cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0��2 | B�� | 1.5��2 | C�� | 1��2 | D�� | 1��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
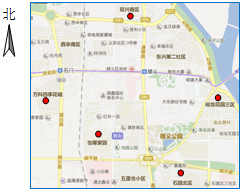 ��ͼ��˳������ͼ��һ���֣�С��������ܰ��С����С�����С���ҵı�ƫ��Լ15�㷽���ϣ���С��ҿ���ס�ڣ�������
��ͼ��˳������ͼ��һ���֣�С��������ܰ��С����С�����С���ҵı�ƫ��Լ15�㷽���ϣ���С��ҿ���ס�ڣ�������| A�� | ԣ�������� | B�� | ˫������ | C�� | ʯ���� | D�� | ����ļ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
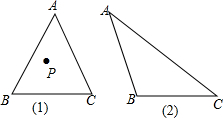 ��Ҫ����ͼ��
��Ҫ����ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com