
【题目】如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=![]() 的图象分别交于C、D两点,点D的坐标为(2,-3),点B是线段AD的中点.则不等式 k1x+b —
的图象分别交于C、D两点,点D的坐标为(2,-3),点B是线段AD的中点.则不等式 k1x+b —![]() >0的解集是___________.
>0的解集是___________.

【答案】x<—4或0<x<2
【解析】分析:把点D的坐标代入y2=![]() 利用待定系数法即可求得反比例函数的解析式,作DE⊥x轴于E,根据题意求得A的坐标,然后利用待定系数法求得一次函数的解析式,联立方程求得C的坐标,根据图象即可求得结论.
利用待定系数法即可求得反比例函数的解析式,作DE⊥x轴于E,根据题意求得A的坐标,然后利用待定系数法求得一次函数的解析式,联立方程求得C的坐标,根据图象即可求得结论.
详解:∵点D(2,﹣3)在反比例函数y2=![]() 的图象上,∴k2=2×(﹣3)=﹣6,∴y2=﹣
的图象上,∴k2=2×(﹣3)=﹣6,∴y2=﹣![]() ;
;
作DE⊥x轴于E.∵D(2,﹣3),点B是线段AD的中点,∴A(﹣2,0).∵A(﹣2,0),D(2,﹣3)在y1=k1x+b的图象上,∴![]() ,解得:k1=﹣
,解得:k1=﹣![]() ,b=﹣
,b=﹣![]() ,∴y1=﹣
,∴y1=﹣![]() x﹣
x﹣![]() ;由
;由 ,解得:
,解得: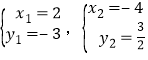 ,∴C(﹣4,
,∴C(﹣4,![]() ), 由图象可知:当x<﹣4或0<x<2时,y1>y2.故答案为:x<—4或0<x<2.
), 由图象可知:当x<﹣4或0<x<2时,y1>y2.故答案为:x<—4或0<x<2.



 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两名同学参加1 000米比赛,由于参赛选手较多,将选手随机分A、B、C三组进行比赛.
(1)甲同学恰好在A组的概率是________;
(2)求甲、乙两人至少有一人在B组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB、CD 是圆O 的两条直径,且∠AOD =α(0° < α < 90°),点P是扇形AOD内任意一点.点P将AB、CD所在直线依次轮流作为对称轴翻折,将点P关于AB对称的点记为点P1 ,点P1关CD 对称的点记为点P2,点 P2 关于AB 对称的点记为点P3,….
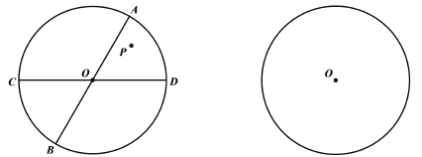
(1)根据所给图中点P 的位置,分别画出点 P 1、P 1;(不写作图步骤,但要保留作图痕迹)
(2)分别联结OP、OP1、OP2,那么线段OP、OP1、OP2 之间的数量关系是:OP OP1 OP2(填空,不要求写出过程);
(3)由(1)、(2)可知,点 P 绕点O旋转可以到达点P2的位置,如果 α=60°,OP= a,求线段 OP顺时针旋转到OP2 过程中扫过的面积;
(4)在 α 取某些特定值的时候,如果按照这样的方式翻折,总能得到一点Pn与点P 重合, 求当n =12,点 P12 与点P 第一次重合时 α 的值.(直接写出结果,不要求写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B、C三地在同一条路上,A地在B地的正南方3千米处,甲、乙两人分别从A、B两地向正北方向的目的地C匀速直行,他们分别和A地的距离s(千米)与所用的时间t(小时)的函数关系如图所示.

(1)图中的线段l1是 (填“甲”或“乙”)的函数图象,C地在B地的正北方向 千米处;
(2)谁先到达C地?并求出甲乙两人到达C地的时间差;
(3)如果速度慢的人在两人相遇后立刻提速,并且比先到者晚1小时到达C地,求他提速后的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于点G,连接AG、HG。下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG。其中,正确的结论有( )

A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,连接AF、BE交于点G,连接CE、DF交于点H.
(1)求证:四边形EGFH为平行四边形;
(2)当![]() = 时,四边形EGFH为矩形。
= 时,四边形EGFH为矩形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:
定义:如果一个数的平方等于,记为![]() ,这个数
,这个数![]() 叫做虚数单位,把形如
叫做虚数单位,把形如![]() (a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部.它的加,减,乘法运算与整式的加,减,乘法运算类似.
(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部.它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:![]() ;
;
![]()
根据以上信息,完成下列问题:
(1)填空:![]() ,
,![]() ;
;
(2)计算:![]() ;
;
(3)计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,O,B依次在直线MN上,如图1,现将射线OA绕点O顺时针方向以每秒10°的速度旋转,同时射线OB绕着点O按逆时针方向以每秒15°的速度旋转,直线MN保持不动,如图2,设旋转时间为t秒(t≤12).
(1)在旋转过程中,当t=2时,求∠AOB的度数.
(2)在旋转过程中,当∠AOB=105°时,求t的值.
(3)在旋转过程中,当OA或OB是某一个角(小于180°)的角平分线时,求t的值.
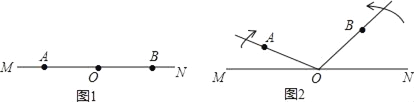
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com