
| ��ֽ���ȷֽ� ���ȷֽ����⣨trisection of an angle���Ƕ�ǧ�İ���ǰ����ϣ��������ļ���������ͼ����֮һ�����ȷ�����ǡ���ԲΪ������������������Բ����ֱ�ߣ�û�п̶ȣ�ֻ����ֱ�ߵij��ӣ���һ��������ȷ֣���������������������ȥ�о�������һ�ɹ���1837�귨����ѧ�ҷ������1814��1848�����ô�������֤���ˣ����ó߹治���E�����ȷֽǣ� �����ͼ����û�����ƣ��������ſ�������������ȷ��ǿ��Խ���ģ��������һ����ֽ���ȷ�������ǵķ����� ��1����������ֽƬ���۳������SBC����������ABCD���ۣ��ۺ�Ϊ��ΪMN���ٽ�����MBCN���ۣ��ۺۼ�ΪEF���õ�ͼ��1���� ��2���������½�ʹ��B��EF�ϵĵ�T�غϣ���M��SB�ϵĵ�P�غϣ���E���ۺ�Ķ�Ӧ���ΪQ���ۺ�Ϊ��ΪGH���õ�ͼ��2���� ��3���۳�����BQ��BT���õ�ͼ��3����������BQ��BT���ǡ�SBC�����ȷ��ߣ�  ������֤��BQ��BT�ǡ�SBC���ȷ��ߵIJ��ֹ��̣� ֤������T��TK��BC������ΪK�����ı���EBKTΪ���� �����۵�����EB=QT����EBT=��QTB��BT=TB ���EBT�ա�QTB�� ���BQT=��TEB=90�㣬 ��BQ��PT �� |
���� ��1��֤��PQ=QT���ó�BP=BT���ɵ��������ε����ʵó���PBQ=��TBQ��֤��TK=TQ���ɵ��������ε����ʵó���QBT=��TBC�����ɵó����ۣ�
��2��ͬ��1����֪������BQ��BT�ǡ�DBC�����ȷ��ߣ���T��TJ��BC������ΪJ�����TBJ=$\frac{1}{3}$��DBC���������ε����ʵó���DBC=45�㣬�����TBJ=15�㣬���۵����ʵã�BH=HT���ó���TBJ=��HTB=15�㣬��THJ=30�㣬��BC=4����BE=1��֤���ı���EBJTΪ���Σ��ó�TJ=BE=1����Rt��THJ�У���THJ=30�㣬��ֱ�������ε����ʵó�HT=2TJ=2�������Ǻ������HJ=cot30��•TJ=$\sqrt{3}$��1=$\sqrt{3}$���ó�BJ=BH+HJ=HT+HJ=2+$\sqrt{3}$���������Ǻ������弴�ɵó��𰸣�
��� �⣺��1��ʣ���֤���������£�
��ME=PQ��EB=QT��ME=EB��
��PQ=QT��
��BP=BT��
���PBQ=��TBQ��
��TK=BE��
��TK=TQ��
���QBT=��TBC��
������BQ��BT�ǡ�SBC�����ȷ��ߣ�
��2��ͬ��1����֪������BQ��BT�ǡ�DBC�����ȷ��ߣ�
��T��TJ��BC������ΪJ����ͼ��ʾ��
���TBJ=$\frac{1}{3}$��DBC��
���ı���ABCDΪ�����Σ�
���DBC=45�㣬
���TBJ=15�㣬
���۵����ʵã�BH=HT��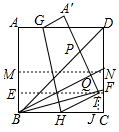
���TBJ=��HTB=15�㣬
���THJ=30�㣬
��BC=4����BE=1��
�߽�������ABCD���ۣ��ۺ�Ϊ��ΪMN���ٽ�����MBCN���ۣ��ۺۼ�ΪEF��TJ��BC��
���ı���EBJTΪ���Σ�
��TJ=BE=1��
��Rt��THJ�У���THJ=30�㣬
��HT=2TJ=2��HJ=cot30��•TJ=$\sqrt{3}$��1=$\sqrt{3}$��
��BJ=BH+HJ=HT+HJ=2+$\sqrt{3}$��tan��TBJ=$\frac{TJ}{BJ}$=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$��
��tan15��=2-$\sqrt{3}$��
�ʴ�Ϊ��2-$\sqrt{3}$��
���� �������ı����ۺ���Ŀ�������������ε����ʡ��۵������ʡ����������ε����ʡ����ε��ж������ʡ�ֱ�������ε����ʡ����Ǻ��������֪ʶ�������ۺ���ǿ����һ���Ѷȣ�


 �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��Ʒ�۸� ������ | 120 | 180 | 200 | 260 |
| ���̳� | 96 | 144 | 160 | 208 |
| ���̳� | 120 | 200 | 200 | ��242 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
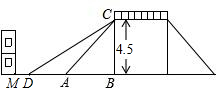 ��ͼ��һ���������ŵ�ʾ��ͼ��CB��DB�����ŵĸ߶�CBΪ4.5�ף�б��AC���½�Ϊ45�㣬Ϊ�˷��������Ƴ������ţ��������ž������ԭб�£�ʹ�½�б��DC���¶�i=1��1.8����D�����������3�������е����ʾ�A��7�Ľ�����M�Ƿ���Ҫ���������B��A��D��M��ͬһֱ���ϣ�
��ͼ��һ���������ŵ�ʾ��ͼ��CB��DB�����ŵĸ߶�CBΪ4.5�ף�б��AC���½�Ϊ45�㣬Ϊ�˷��������Ƴ������ţ��������ž������ԭб�£�ʹ�½�б��DC���¶�i=1��1.8����D�����������3�������е����ʾ�A��7�Ľ�����M�Ƿ���Ҫ���������B��A��D��M��ͬһֱ���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
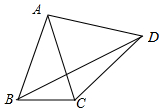 ��ͼ����ABC�У�AB=AC=5��BC=2����ACΪ���ڡ�ABC�����ȱ�������ACD������BD����BD=$\sqrt{3}$+2$\sqrt{6}$��
��ͼ����ABC�У�AB=AC=5��BC=2����ACΪ���ڡ�ABC�����ȱ�������ACD������BD����BD=$\sqrt{3}$+2$\sqrt{6}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O��ֱ������C��AB���ӳ����ϣ�CD�С�O�ڵ�D������AD����A=28�㣬���C=34�ȣ�
��ͼ��AB�ǡ�O��ֱ������C��AB���ӳ����ϣ�CD�С�O�ڵ�D������AD����A=28�㣬���C=34�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��ƽ��ֱ������ϵ�У���֪A��2��3����B��3��5������PΪֱ��y=x-2��һ�����㣬��|PB-PA|ֵ���ʱ����P������Ϊ��-1��-3����
��֪��ƽ��ֱ������ϵ�У���֪A��2��3����B��3��5������PΪֱ��y=x-2��һ�����㣬��|PB-PA|ֵ���ʱ����P������Ϊ��-1��-3�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com