
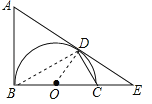
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
(3)若∠CDE=27°,OB=2,求![]() 的长.
的长.

【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)连接OD,BD,根据圆周角定理得到∠ABO=90°,根据等腰三角形的性质得到∠ABD=∠ADB,∠DBO=∠BDO,根据等式的性质得到∠ADO=∠ABO=90°,根据切线的判定定理即可得到即可;
(2)由AD是半圆O的切线得到∠ODE=90°,于是得到∠ODC+∠CDE=90°,根据圆周角定理得到∠ODC+∠BDO=90°,等量代换得到∠DOC=2∠BDO,∠DOC=2∠CDE即可得到结论;
(3)根据已知条件得到∠DOC=2∠CDE=54°,根据平角的定义得到∠BOD=180°﹣54°=126°,然后由弧长的公式即可计算出结果.
试题解析:(1)证明:连接OD,BD,∵AB是⊙O的直径,∴AB⊥BC,即∠ABO=90°,∵AB=AD,∴∠ABD=∠ADB,∵OB=OD,∴∠DBO=∠BDO,∴∠ABD+∠DBO=∠ADB+∠BDO,∴∠ADO=∠ABO=90°,∴AD是半圆O的切线;
(2)证明:由(1)知,∠ADO=∠ABO=90°,∴∠A=360°﹣∠ADO﹣∠ABO﹣∠BOD=180°﹣∠BOD,∵AD是半圆O的切线,∴∠ODE=90°,∴∠ODC+∠CDE=90°,∵BC是⊙O的直径,∴∠ODC+∠BDO=90°,∴∠BDO=∠CDE,∵∠BDO=∠OBD,∴∠DOC=2∠BDO,∴∠DOC=2∠CDE,∴∠A=∠CDE;
(3)解:∵∠CDE=27°,∴∠DOC=2∠CDE=54°,∴∠BOD=180°﹣54°=126°,∵OB=2,∴![]() 的长=
的长=![]() =
=![]() .
.


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE. 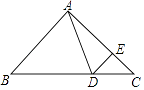
(1)当∠BAD=60°,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试写出∠BAD与∠CDE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
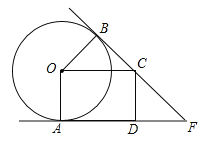
【题目】如图,PA,PB是⊙O的切线,A,B为切点,点C在PB上,OC∥AP,CD⊥AP于D
(1)求证:OC=AD;
(2)若∠P=50°,⊙O的半径为4,求四边形AOCD的周长(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角∠AOB,∠COD有相同的顶点O,下列结论:①∠AOC=∠BOD;
②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线. 其中正确的个数有( )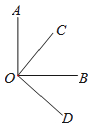
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)解不等式 ![]() >1﹣
>1﹣ ![]() ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
(2)一个长方形足球训练场的长为xm,宽为70m.如果它的周长大于350m,面积小于7560m2 , 请确定x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com