
【题目】如图,数轴上点![]() 、
、![]() 表示的有理数分别为-10、5,点
表示的有理数分别为-10、5,点![]() 是射线
是射线![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合),点
重合),点![]() 是线段
是线段![]() 靠近点
靠近点![]() 的三等分点,点
的三等分点,点![]() 是线段
是线段![]() 靠近点
靠近点![]() 的三等分点.
的三等分点.
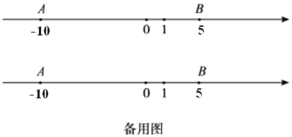
(1)若点![]() 表示的有理数是0,那么
表示的有理数是0,那么![]() 的长为______;若点
的长为______;若点![]() 表示的有理数是1,那么
表示的有理数是1,那么![]() 的长为______.
的长为______.
(2)点![]() 在射线
在射线![]() 上运动(不与点
上运动(不与点![]() 、
、![]() 重合)的过程中,
重合)的过程中,![]() 的长是否发生改变?若不改变,请求出
的长是否发生改变?若不改变,请求出![]() 的长;若改变,请说明理由.
的长;若改变,请说明理由.
【答案】(1)10,10;(2)![]() 的长不会发生改变,且
的长不会发生改变,且![]() .
.
【解析】
(1)由点P表示的有理数为0可得出AP、BP的长度,根据三等分点的定义可得出MP、NP的长度,再由MN=MP+NP即可求出MN的长度;当点P表示的有理数为1时,利用同样的方法求解即可;
(2)设点P表示的有理数是a(a>﹣10且a≠5),分﹣10<a<5及a>5两种情况考虑,由点P表示的有理数可得出AP、BP的长度(用含字母a的代数式表示),根据三等分点的定义可得出MP、NP的长度(用含字母a的代数式表示),再由MN=MP+NP(或MN=MP﹣NP),即可求出MN的长,进而可作出判断.
解:(1)若点P表示的有理数是0,则AP=10,BP=5.
∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.
∴MP=![]() AP=
AP=![]() ,NP=
,NP=![]() BP=
BP=![]() ,
,
∴MN=MP+NP=![]() +
+![]() =10;
=10;
若点P表示的有理数是1,则AP=11,BP=4.
∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点,
∴MP=![]() AP=
AP=![]() ,NP=
,NP=![]() BP=
BP=![]() ,
,
∴MN=MP+NP=![]() +
+![]() =10.
=10.
故答案为:10,10;
(2)MN的长不会发生改变,理由如下:
设点P表示的有理数是a(a>﹣10且a≠5).
当﹣10<a<5时,如图1,AP=a+10,BP=5﹣a.
∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.
∴MP=![]() AP=
AP=![]() (a+10),NP=
(a+10),NP=![]() BP=
BP=![]() (5﹣a),
(5﹣a),
∴MN=MP+NP=![]() (a+10)+
(a+10)+![]() (5﹣a)=10;
(5﹣a)=10;

当a>5时(如图2),AP=a+10,BP=a﹣5.
∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.
∴MP=![]() AP=
AP=![]() (a+10),NP=
(a+10),NP=![]() BP=
BP=![]() ( a﹣5),
( a﹣5),
∴MN=MP﹣NP=![]() (a+10)-
(a+10)-![]() ( a﹣5)=10.
( a﹣5)=10.
综上所述:点P在射线AB上运动(不与点A,B重合)的过程中,MN的长不会发生变化,且为定值10.



科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,﹣1),C(﹣2,﹣1),D(﹣1,1).以A为对称中心作点P(0,2)的对称点P1,以B为对称中心作点P1的对称点P2,以C为对称中心作点P2的对称点P3,以D为对称中心作点P3的对称点P4,…,重复操作依次得到点P1,P2,…,则点P2010的坐标是( )
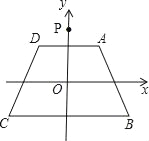
A. (2010,2) B. (2010,﹣2) C. (2012,﹣2) D. (0,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
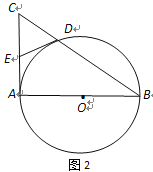
【题目】已知AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点D(如图1).
(1)若AB=2,∠B=30°,求CD的长;
(2) 取AC的中点E,连结D、E(如图2),求证:DE与⊙O相切.

【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】分析:![]() 连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得
连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得![]() 的长度.
的长度.
![]() 连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到
连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到
∠ODA=∠DAO,得到∠EDA+∠ODA=∠EAD+∠DAO.得到∠EDO=90°即可.
详解:(1)如图,连接AD ,
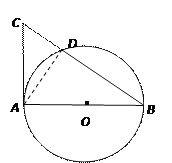
∵AC是⊙O的切线,AB是⊙O的直径,
∴∠CAB=∠ADB=90°,
∴ΔCAB,ΔCAD均是直角三角形.
∴∠CAD=∠B=30°.
在RtΔCAB中,AC=ABtan30°=![]()
∴在RtΔCAD中,CD=ACsin30°=![]()
(2)如图,连接OD,AD.

∵AC是⊙O的切线,AB是⊙O的直径,
∴∠CAB=∠ADB=∠ADC=90°,
又∵E为AC中点,
∴DE=CE=EA,
∴∠EDA=∠EAD.
∵OD=OA,
∴∠ODA=∠DAO,
∴∠EDA+∠ODA=∠EAD+∠DAO.
即:∠EDO=∠EAO=90°.
又点D在⊙O上,因此DE与⊙O相切.
点睛:考查解直角三角形,圆周角定理,切线的判定与性质等,属于圆的综合题,比较基础.注意切线的证明方法,是高频考点.
【题型】解答题
【结束】
21
【题目】课外活动时间,甲、乙、丙、丁4名同学相约进行羽毛球比赛.
(1)如果将4名同学随机分成两组进行对打,求恰好选中甲乙两人对打的概率;
(2)如果确定由丁担任裁判,用“手心、手背”的方法在另三人中竞选两人进行比赛.竞选规则是:三人同时伸出“手心”或“手背”中的一种手势,如果恰好只有两人伸出的手势相同,那么这两人上场,否则重新竞选.这三人伸出“手心”或“手背”都是随机的,求一次竞选就能确定甲、乙进行比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
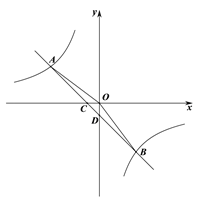
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数图象交于第二,四象限内A,B两点,与![]() 轴交于点C,与
轴交于点C,与![]() 轴交于点D.若点B的纵坐标为
轴交于点D.若点B的纵坐标为![]() ,OA=5,
,OA=5, ![]() .
.
(1)求反比例函数解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
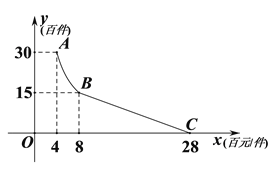
【题目】2017年元旦莫小贝在襄阳万达广场购进一家商铺,装修后用于销售某品牌的女装.2018元旦莫小贝盘点时发现:2017年自家店内女装的平均成本为4百元/件,当年的销售量![]() (百件)与平均销售价格
(百件)与平均销售价格![]() (百元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.
(百元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.
(1)请求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若莫小贝购商铺及装修一共花了120万元,请通过计算说明2017年莫小贝是赚还是亏?若赚,最多赚多少元?若亏,最少亏多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察表格:
|
|
| |
1条直线 0个交点 平面分成(1+1)块 | 2条直线 1个交点 平面分成(1+1+2)块 | 3条直线 (1+2)个交点 平面分成(1+1+2+3)块 | 4条直线 (1+2+3)个交点 平面分成(1+1+2+3+4)块 |
根据表格中的规律解答问题:
(1)5条直线两两相交,有 个交点,平面被分成 块;
(2)n条直线两两相交,有 个交点,平面被分成 块;
(3)应用发现的规律解决问题:一张圆饼切10刀(不许重叠),最多可得到 块饼.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:
A.仅学生自己参与 B.家长和学生一起参与
C.仅家长自己参与 D.家长和学生都未参与
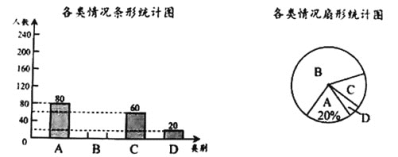
请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了_________名学生;
(2)补全条形统计图,并在扇形统计图中计算类所对应扇形的圆心角的度数.
(3)根据抽样调查结果,估计该校1500名学生中“家长和学生都未参与”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市,第23题,10分)湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批淡水鱼放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为![]() ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.
①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com