
问题探究
⑴ 请在图①中作出两条直线,使它们将圆的面积四等分;
⑵ 如图②,M是正方形ABCD内一定点,请在图②中作出两条直线(要求其中一条直线必须过点M),使它们将正方形ABCD的面积四等分,并说明理由.
问题解决
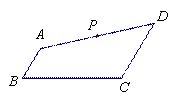
⑶ 如图③,在四边形ABCD中,AB∥CD,AB+CD=BC,点P是AD的中点.如果AB= ,CD=
,CD=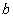 ,且
,且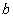 >
> ,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?若存在,求出BQ的长;若不存在,说明理由.
,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?若存在,求出BQ的长;若不存在,说明理由.
 | |||||
 | |||||
 | |||||
| |||||
|
| ||||
| |
解:(1)如图1所示,( 只要两直线互相垂直) 
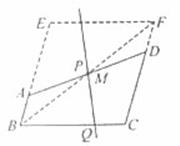
(2)连接AC、BD交于O,作直线OM,分别交AD于P,交BC于Q,过O作EF⊥OM交DC于F,交AB于E,则直线EF、OM将正方形的面积四等份,
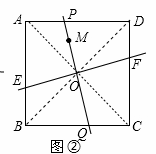 理由是:∵点O是正方形ABCD的对称中心,
理由是:∵点O是正方形ABCD的对称中心,
∴AP=CQ,EB=DF,
在△AOP和△EOB中
∵∠AOP=90°-∠AOE,∠BOE=90°-∠AOE,
∴∠AOP=∠BOE,
∵OA=OB,∠OAP=∠EBO=45°,
∴△AOP≌△EOB,
∴AP=BE=DF=CQ,
设O到正方形ABCD一边的距离是d,
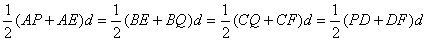
∴S四边形AEOP=S四边形BEOC=S四边形CQOF=S四边形DPOF,
直线EF、OM将正方形ABCD面积四等份;
(3)存在,当BQ=CD=b时,PQ将四边形ABCD的面积二等份,
方法一:如图③,连接BP并延长交CD的延长线于点E,
∵AB∥CD,
∴∠A=∠EDP,∵在△ABP和△DEP中,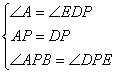 ,
,
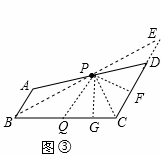 ∴△ABP≌△DEP(ASA),
∴△ABP≌△DEP(ASA),
∴BP=EP,
连接CP,
∵△BPC的边BP和△EPC的边EP上的高相等,
又∵BP=EP,
∴S△BPC=S△EPC,
作PF⊥CD,PG⊥BC,则BC=AB+CD=DE+CD=CE,
由三角形面积公式得:PF=PG,
在CB上截取CQ=DE=AB=a,则S△CQP=S△DEP=S△ABP
∴S△BPC-S△CQP+S△ABP=S△CPE-S△DEP+S△CQP
即:S四边形ABQP=S四边形CDPQ,
∵BC=AB+CD=a+b,
∴BQ=b,
∴当BQ=b时,直线PQ将四边形ABCD的面积分成相等的两部分.


科目:初中数学 来源: 题型:
为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备精加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍;
信息三:甲工厂加工一天、乙工厂加工2天共需加工费11200元,甲工厂加工 2天、乙工厂加工3天共需加工费18400元;
2天、乙工厂加工3天共需加工费18400元;
根据以上信息,完成下列问题:
(1)求甲、乙两个工厂每天分别能加工多少件新产品?
(2)公司将1200件新产品交甲、乙两工厂一起加工3天后,根据产品质量和市场需求,决定将剩余产品交乙工厂单独加工,求该公司这批产品的加工费用为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com