
【题目】菱形ABCD的边长是4,∠DAB=60,点M,N分别在边AD,AB上,MN⊥AC,垂足为P,把△AMN沿MN折叠得到△A'MN,若△A'DC恰为等腰三角形,则AP的长为_____。

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,O是对角线AC、BD的交点,过点O作OE⊥OF,分别交AB、BC于E. F.

(1)求证:△OEF是等腰直角三角形。
(2)若AE=4,CF=3,求EF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)|﹣2|+|﹣10|﹣|﹣5|
(2)(﹣3.5)+(+8![]() )﹣(﹣5.5)+(﹣2
)﹣(﹣5.5)+(﹣2![]() )
)
(3)﹣42+3×(﹣2)2×(![]() -1)÷(﹣1
-1)÷(﹣1![]() )
)
(4)(![]() ﹣
﹣![]() ﹣
﹣![]() )×(﹣24)+42÷(﹣2)3+(﹣1)2019
)×(﹣24)+42÷(﹣2)3+(﹣1)2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像经过点A(-1,0),并与反比例函数
的图像经过点A(-1,0),并与反比例函数![]() (
(![]() )的图像交于B(m,4)
)的图像交于B(m,4)

(1)求![]() 的值;
的值;
(2)以AB为一边,在AB的左侧作正方形![]() ,求C点坐标;
,求C点坐标;
(3)将正方形![]() 沿着
沿着![]() 轴的正方向,向右平移n个单位长度,得到正方形
轴的正方向,向右平移n个单位长度,得到正方形![]() ,线段
,线段![]() 的中点为点
的中点为点![]() ,若点
,若点![]() 和点
和点![]() 同时落在反比例函数
同时落在反比例函数![]() 的图像上,求n的值.
的图像上,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)36+(-25)+12+(-15);
(2) 9+(-2.5)+(+6)+(-3.5);
(3)3.7+(-9.1)+6.3+(-0.9) ;
(4)10-(-5)-(-6)-(+18)
(5)(-12)-6-(-8)-(-12);
(6)5-(-5)+(-10)+0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快城市群的建设与发展,在A、B两城市间新建一条城际铁路,建成后,铁路运行里程由现在的210km缩短至180km,平均时速要比现行的平均时速快200km,运行时间仅是现行时间的![]() ,求建成后的城际铁路在A、B两地的运行时间?
,求建成后的城际铁路在A、B两地的运行时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点表示数b,C点表示数C,b是最小的正整数,且a=﹣2,c=7.
(1)若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合;
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.
则AB= ,AC= ,BC= .(用含t的代数式表示)
(3)请问:3BC﹣2AB的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解(solution).已知:关于![]() 的方程
的方程![]() .
.
(1)若![]() 是方程
是方程![]() 的解,求
的解,求![]() 的值;
的值;
(2)若关于![]() 的方程
的方程![]() 的解比方程
的解比方程![]() 的解大6,求
的解大6,求![]() 的值;
的值;
(3)若关于![]() 的方程
的方程![]() 与
与![]() 均无解,求代数式
均无解,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,点P从点A出发,以1cm/s的速度沿折线AC→CB→BA运动,最终回到点A,设点P的运动时间为x(s),线段AP的长度为y(cm),则能够反映y与x之间函数关系的图象大致是( )

A.  B.
B. 
C. 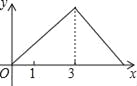 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com