
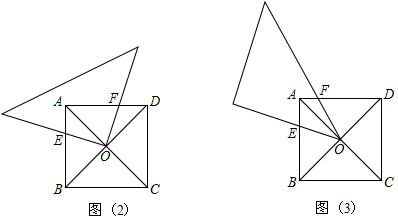
如图(1),一正方形纸板ABCD的边长为4,对角线AC、BD交于点O,一块等腰直角三角形的三角板的一个顶点处于点O处,两边分别与线段AB、AD交于点E、F,设BE= .
.
(1)若三角板的直角顶点处于点O处,如图(2).判断三角形EOF的形状 ,并说明理由。
,并说明理由。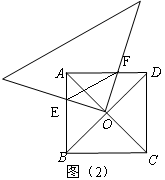
(2)在(1)的条件下,若三角形EOF的面积为S,求S关于x的函数关系式。
(3)若三角板的锐角顶点处于点O处,如图(3).
①若DF=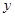 ,求
,求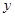 关于
关于 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
②探究直线EF与正方形ABCD的内切圆的位置关系,并证明你的结论.
(1)△EOF是等腰直角三角形,(2)S=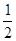 x2-2x+4 (3)EF与正方形ABCD的内切圆相切。
x2-2x+4 (3)EF与正方形ABCD的内切圆相切。
解析试题分析:解:(1)∵正方形ABCD∴∠AOB=∠EOF=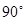 ,BO=AO=OD,
,BO=AO=OD,
∠OAF=∠OBE= ∴∠AOF=∠BOE∴△AOF≌△BOE
∴∠AOF=∠BOE∴△AOF≌△BOE
∴OE=OF ∴三角形EOF是等腰直角三角形。
(2)由△AOF≌△BOE得BE=AF,AE=FD=

∵ ∴
∴
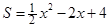
(3)①∵∠EOF=∠0BE= ∴∠FOD+∠EOB=∠BEO+∠EOB=
∴∠FOD+∠EOB=∠BEO+∠EOB=
∴∠FOD=∠BEO,又∠EBO=∠ODF= ∴△BOE∽△DFO
∴△BOE∽△DFO
∴ ∴
∴
(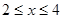 )
)
②连结EF
由①知△BOE∽△DFO
∴ ∵BO=DO
∵BO=DO
∴ 而∠EOF=∠0BE=
而∠EOF=∠0BE=
∴△EOF∽△EBO,∴∠FEO=∠0EB
∴点O到EF、BE的距离相等,而O到BE的距离即为正方形内切
圆⊙O的半径
∴直线EF与正方形的内切圆相切
考点:正方形的定义及性质,等腰三角形定义及性质,勾股定理,相似三角形判定及性质,切线的定义。
点评:熟知以上的定义性质,定理。本题应用的知识面很广,对学生要求很高,要认真的体会,把知识点很好的结合在一起,本题难度较大问多,属于偏难题。


科目:初中数学 来源: 题型:
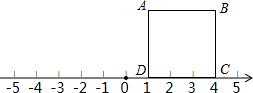
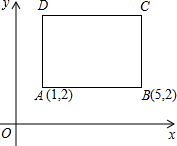 如图,四边形ABCD是一正方形,已知A(1,2),B(5,2)
如图,四边形ABCD是一正方形,已知A(1,2),B(5,2)查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com