
���� ��1�����ݸ����б�ʽ��=��k+1��2��0������֤������������ʵ������
��2���跽�̵������ֱ�Ϊx1��x2�����ݸ���ϵ���Ĺ�ϵ���ɵó�x1+x2=$\frac{k-1}{k}$���ٸ�������ʵ������Ϊ�෴�����ɵó�����k�ķ�ʽ���̣��ⷽ�̼��ɵó�k��ֵ��
��3������ʮ����˷��������x1=-$\frac{1}{k}$��x2=1�����ݷ�������������������Ķ��弴�ɵó�����k�IJ���ʽ���ⲻ��ʽ�������k��ȡֵ��Χ��
��� ��1��֤�������ڷ���kx2-��k-1��x-1=0��k��0���У���=[-��k-1��]2-4��k����-1��=��k+1��2��0��
���������ʵ������
��2���⣺�跽�̵������ֱ�Ϊx1��x2����x1+x2=$\frac{k-1}{k}$��
��x1��x2��Ϊ�෴����
��$\frac{k-1}{k}$=0����ã�k=1��
����֤k=1�Ƿ���$\frac{k-1}{k}$=0�Ľ⣮
�൱k=1ʱ���˷��̵�����ʵ������Ϊ�෴����
��3���⣺��kx2-��k-1��x-1=��kx+1����x-1��=0��
��x1=-$\frac{1}{k}$��x2=1��
�߹���x��һԪ���η���kx2-��k-1��x-1=0�����������������
��2��-$\frac{1}{k}$��3��2��$\frac{1}{-\frac{1}{k}}$=-k��3��
��ã�-$\frac{1}{2}$��k��-$\frac{1}{3}$��-3��k��-2��
���� ���⿼���˸����б�ʽ������ϵ���Ĺ�ϵ�Լ���һԪһ�β���ʽ���������ո���ϵ���Ĺ�ϵ�Լ������б�ʽ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
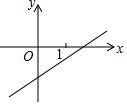 һ�κ���y=kx+b��ͼ����ͼ��ʾ���������ж���ȷ���ǣ�������
һ�κ���y=kx+b��ͼ����ͼ��ʾ���������ж���ȷ���ǣ�������| A�� | |k|��|b| | B�� | |k|��|b| | ||
| C�� | |k|=|b| | D�� | |k|��|b|�Ĵ�С��ϵ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
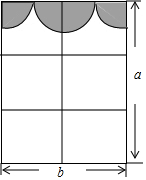 ij���䴰����ͼ��ʾ�������Ϸ���װ�����������ķ�֮һԲ��һ����Բ��ɣ����ǵİ뾶��ͬ����
ij���䴰����ͼ��ʾ�������Ϸ���װ�����������ķ�֮һԲ��һ����Բ��ɣ����ǵİ뾶��ͬ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
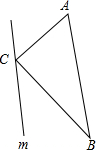 ��ͼ���ڡ�ABC�У�AB=10��AC=6��BC=8����ֱ��m��AB����AB��ֱ��m֮��ľ���Ϊ$\frac{24}{5}$��
��ͼ���ڡ�ABC�У�AB=10��AC=6��BC=8����ֱ��m��AB����AB��ֱ��m֮��ľ���Ϊ$\frac{24}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com