
【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
【答案】
(1)解:∵BC=DC,
∴∠CBD=∠CDB=39°,
∵∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,
∴∠BAD=∠BAC+∠CAD=39°+39°=78°.
(2)证明:∵EC=BC,
∴∠CEB=∠CBE,
又∵∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,
∴∠2+∠BAE=∠1+∠CBD,
∵∠BAE=∠BDC=∠CBD,
∴∠1=∠2.
【解析】(1)由等腰三角形的性质得∠CBD=∠CDB=39°,再根据同弧所对的圆心角相等得∠BAC=∠CDB=∠CAD=∠CBD=39°,从而求出∠BAD值.
(2)由等腰三角形的性质得∠CEB=∠CBE,又由∠CEB=∠2+∠BAE=∠CBE=∠1+∠CBD,由等量代换及等式额性质得∠1=∠2.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度,进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
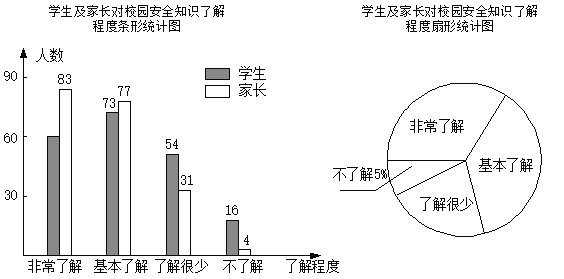
(1)参与调查的学生及家长共有 人;
(2)在扇形统计图中,“基本了解”所对应的圆心角的度数是 ;
(3)在条形统计图中,“非常了解”所对应的学生人数是 ;
(4)若全校有1200名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的顶点A,B,C的坐标分别是A(﹣1,﹣1),B(﹣4,﹣3),C(﹣4,﹣1).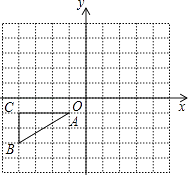
①作出△ABC关于原点O中心对称的图形;
②将△ABC绕原点O按顺时针方向旋转90°后得到△A1B1C1 , 画出△A1B1C1 , 并写出点A1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
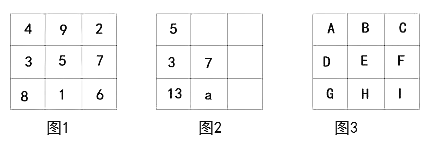
【题目】将9个数填入幻方的九个格中,使处于同一横行、同一竖列、同一斜对角线上的三个数的和相等,如图1所示。
(1)如图2所示,求![]() 的值;
的值;
(2)如图3所示:
①若![]() 求整式D;
求整式D;
②若![]() 求这九个整式的和是多少。
求这九个整式的和是多少。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.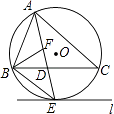
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形如图2.
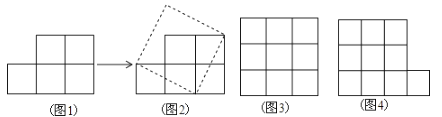
(1)你能在![]() 方格图(图3)中,连接四个格点(网格线的交点)组成面积为5的正方形吗?若能,请用虚线画出.
方格图(图3)中,连接四个格点(网格线的交点)组成面积为5的正方形吗?若能,请用虚线画出.
(2)你能把十个小正方形组成的图形纸(图4),剪开并拼成正方形吗?若能,请仿照图2的形式把它重新拼成一个正方形.
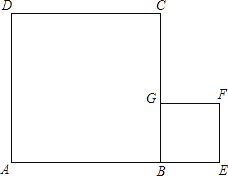
(3)如图,是由两个边长不等的正方形纸片组成的一个图形,要将其剪拼成一个既不重叠也无空隙的大正方形,则剪出的块数最少为________块.请你在图中画出裁剪线,并说明拼接方法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com