
【题目】如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是 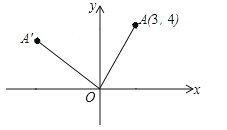
【答案】(﹣4,3)
【解析】解:如图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,
∵OA绕坐标原点O逆时针旋转90°至OA′,
∴OA=OA′,∠AOA′=90°,
∵∠A′OB′+∠AOB=90°,∠AOB+∠OAB=90°,
∴∠OAB=∠A′OB′,
在△AOB和△OA′B′中,![]() ,
,
∴△AOB≌△OA′B′(AAS),
∴OB′=AB=4,A′B′=OB=3,
∴点A′的坐标为(﹣4,3).
故答案为:(﹣4,3).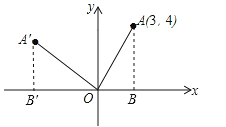
过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,根据旋转的性质可得OA=OA′,利用同角的余角相等求出∠OAB=∠A′OB ′,然后利用“角角边”证明△AOB和△OA′B′全等,根据全等三角形对应边相等可得OB′=AB,A′B′=OB,然后写出点A′的坐标即可.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的两格中,点A、B、C都是格点.
(1)将△ABC向左平移6个单位长度得到得到△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2 , 请画出△A2B2C2;
(3)若点O的坐标为(0,0),点B的坐标为(2,3);写出△A1B1C1与△A2B2C2的对称中心的坐标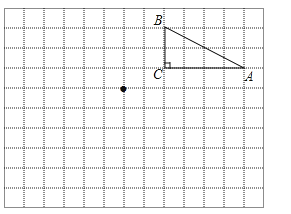
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旧车交易市场有一辆原价为12万元的轿车,已使用3年,如果第一年的折旧率为20%,后其折旧率有所变化,现知第三年末这辆轿车值7.776万元.假设这辆车第二、第三年平均每年的折旧率都相同,那么这辆车第二、第三年平均每年的折旧率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五四”青年节,市团委组织部分中学的团员去西山植树.某校九年级(3)班团支部领到一批树苗,若每人植4棵树,还剩37棵;若每人植6棵树,则最后一人有树植,但不足3棵,这批树苗共有__棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线y=
与双曲线y=![]() 交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=
交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=![]() 上一点,且点C在直线
上一点,且点C在直线![]() 的上方.
的上方.

(1)求双曲线的函数解析式;
(2)若△AOC的面积为6,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线AB上有一点P,点M、N分别为线段PA、PB的中点,AB=14.
(1)若点P在线段AB上,且AP=8,求线段MN的长度; ![]()
(2)若点P在直线AB上运动,设AP=x,BP=y,请分别计算下面情况时MN的长度: ①当P在AB之间(含A或B);
②当P在A左边;
③当P在B右边;你发现了什么规律?
(3)如图2,若点C为线段AB的中点,点P在线段AB的延长线上,下列结论:① ![]() 的值不变;②
的值不变;② ![]() 的值不变,请选择一个正确的结论并求其值.
的值不变,请选择一个正确的结论并求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() 与
与![]() 轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程![]() 的两个根.
的两个根.
(1)请直接写出点A、B的坐标,并求出该二次函数的解析式.
(2)如图1,在二次函数对称轴上是否存在点P,使![]() 的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
(3)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合). 过点Q作QD∥AC交于BC点D,设Q点坐标(m,0),当![]() 面积S最大时,求m的值.
面积S最大时,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com